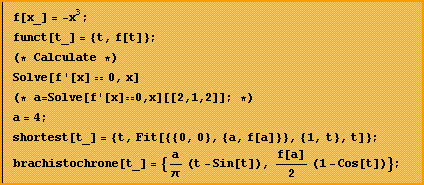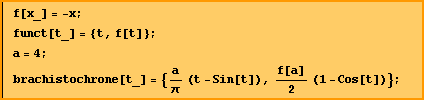The Brachistochrone

The Famous Problem of Fastest Descent: A Classic among All Classics

The NCB invites you to join Galileo, Newton, Leibniz, Huygens, l'Hôpital, and two Bernoullis in thinking about one of the most celebrated problems of 17th century mathematics. The word "brachistochrone" is from the Greek meaning "shortest" and "time."

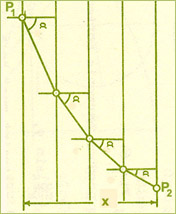
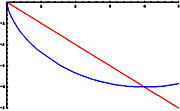Descent curves

What is the path - curve - producing the shortest possible time for a particle to descend from a given point to another point not directly below the start? Will it be a straight line, an arc of a circle, or just what? Will it be a minimum of a function? The shortest distance between two points is a line, but the descent of a weighted particle is acted upon, in the very least, by gravity. A bead descending a wire is often used to depict the pathway, but investigators usually ignore friction.

The correct answer is that a body takes less time to fall along the arc of a circumference than to fall along the "line" of a corresponding chord.

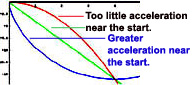
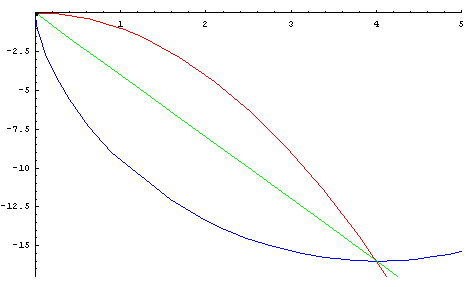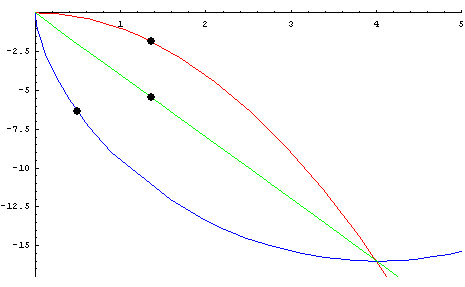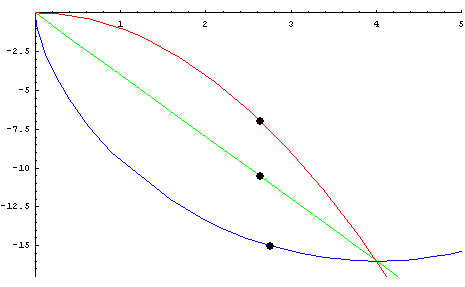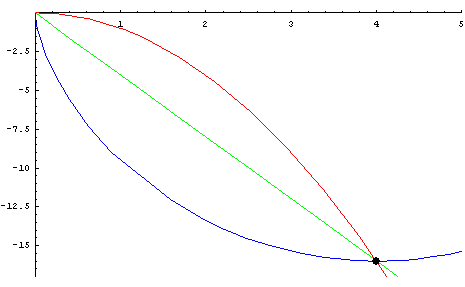
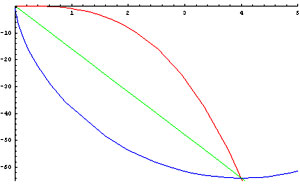
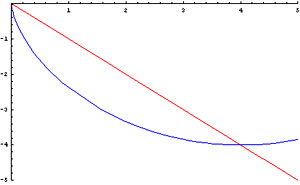
The cycloid path allows the particle to move rapidly at first, while in steep descent, and thus build up sufficient speed to overcome the greater distance the particle must travel. Thus, the speed of the descending particle is accelerated by gravity.

We begin by introducing a MATHEMATICA® animation.

Our animations feature several

Classic Curves "racing"
the corresponding brachistochrone.

You also need to be familiar with the cycloid. A cycloid is the locus of a point on the circumference of a circle rotating along a fixed line . . . .

Animated Cycloid

Play this animation.

and its equations in parametric form are . . . .

Snell's
Law for the Refraction
of Light
is often applied in
deriving the equations.

A lengthy discussion of the equations
is found on two other pages.

Brachistochrone Part II
Brachistochrone Part IV

A reproduction of the original Acta figures (1697) is found on Brachistochrone Part III

Other MATHEMATICA^® Animations

Play this animation.	Play this animation.
Suggestions for other MATHEMATICA^® codes are on these links. [ Please see Stan Wagon, (1991) p. 63, p. 386, for additional discussion of the comparison of the brachistochrone's descent to other curves of degree 1,2,3,6, and 10.] Complete code And in another window . . . . Complete code and still a third window. Complete code

Useful Links and Books

The brachistochrone and cycloid have a very rich math and physics literature.
The National Curve Bank also has MAPLE animations of the cycloid family of curves.

John (Jean, Johann)
Bernoulli

A large statue of Leibniz is at
the Royal Academy of Arts
in the heart of fashionable London.
Note the English chose to spell
his name as . . . .

Leibniz spelling

Beckmann, Petr, A History of π (PI), St. Martin's Press, 1971, pp. 139-140.

Burton, David M., The History of Mathematics, 5th ed., McGraw Hill, 2003, p. 446.

The brachistochrone is for "the shrewdest mathematicians of all the world."

John Bernoulli, June, 1696

Eves, Howard, AN INTRODUCTION TO THE HISTORY OF MATHEMATICS, 6th ed., Saunders College Publishing, 1992, p. 426.

Leibniz: "Splendid problem."

Johnson, Nils P., The Brachistochrone Problem, The College Mathematics Journal, vol. 35 (3), May 2004, pp. 192-197.

A cycloid has the noteworthy property that the time it takes from any point along it to its lowest point does not depend on the starting point.

Johnson and others suggest the Euler-Lagrange formula and boundary conditions applied to the brachistochrone will define a differential equation whose solution is similar to finding critical points (usually a maximum or minimum) in ordinary calculus. "Thus a global problem - an integral over a path - has a local constraint - a differential equation -which dictates the solution at each point along the way."

Lockwood, E. H., A Book of CURVES, Cambridge University Press, 1961, p. 88.

Katz, Victor J., A History of Mathematics, 2nd ed., Addison Wesley Longman, 1998, pp. 547-549, 562.
Katz, Victor J., A History of Mathematics, Brief ed., Pearson Addison Wesley, 2004, pp. 250, 331-332.

Simmons, George F., Calculus Gems: Brief Lives and Memorable Mathematics, McGraw-Hill,1992, pp. 308-313.

"Bernoulli's vivid, enthusiastic, personal style is in sharp contrast to the dead, gray, impersonal style of most of the writing in scientific journals nowadays."

Simmons

"With justice we admire Huygens because he first discovered that a heavy particle slides down to the bottom of a cycloid in the same time, no matter where it starts. But you will be petrified with astonishment when I say that this very same cycloid, the tautochorone of Huygens is also the brachistochrone we are seeking."

Johann Bernoulli

Szapiro, Ben, Revisiting A Classic Least Time Problem,
< http://www.sewanee.edu/physics/TAAPT/TAAPTTALK.html >

Stewart, James, Calculus, 5th ed., THOMSONBrooks/Cole, 2003, p. 691.

"One of the first people to study the cycloid was Galileo, who proposed that bridges be built in the shape of cycloids and who tried to find the area under one arch of a cycloid."

Wagon, Stan, MATHEMATICA^®IN ACTION, W. H. Freeman and Co., 1991, pp. 60-66 and 385-389. ISBN 0-7167-2229-1 or ISBN 0-7167-2202-X (pbk.)
Wagon, Stan, MATHEMATICA® IN ACTION, 2nd ed., Springer-Verlag, 2000. ISBN 0-387-98684-7 for other animations.

Weisstein, Eric W., CRC Concise Encyclopedia of MATHEMATICS, CRC Press, 1999.

"The brachistochrone was one of the earliest problems posed in the Calculus of Variations."

Yates, Robert C., Curves and Their Properties, NCTM, 1952, pp. 68-69.

MATHEMATICA^® Code and animations contributed by
Gustavo Gordillo
2005.
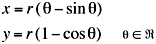