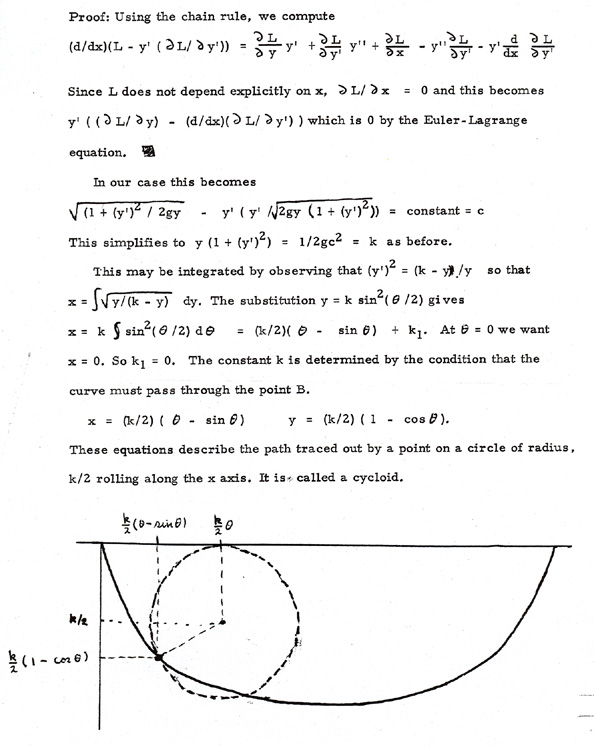
Equations
for the Brachistochrone
The
following are notes prepared for the undergraduate Analysis
class MATH
466, Advanced Calculus II, at California State University, Los
Angeles. The intent was to give the students a taste of
the uses
of some of the Analysis they had learned. The National Curve Bank - A MATH
Archive
thanks Dr.
Michael Hoffman for
making the Euler-Lagrange approach to the brachistochrone
available to
others. [mhoffma@calstatela.edu]The
Brachistochrone Problem
|
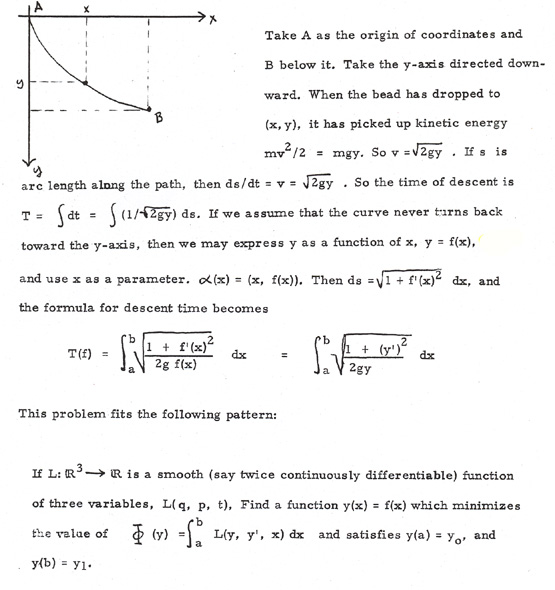
Suppose
A and B are two points,
A lower
than B. Find the shape of the
wire joining them such that a frictionless bead
sliding from
A to B
does so in minimum time.
|
|
|
|
|
|