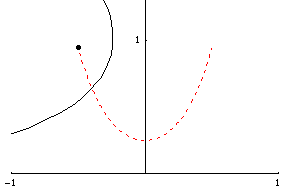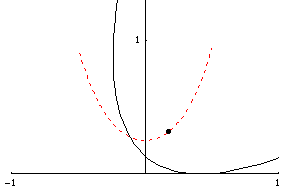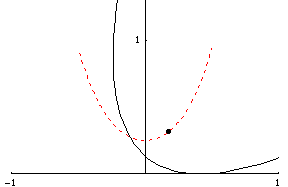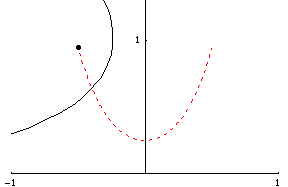
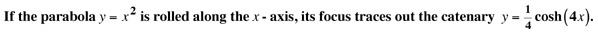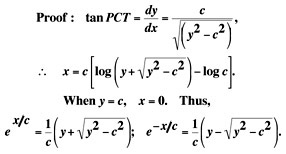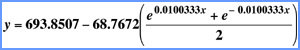The Catenary - The "Chain" Curve

For the Catenary . . . .

Definition:

The catenary is the form assumed by a perfectly flexible inextensible chain of uniform density hanging from two supports not in the same vertical line.

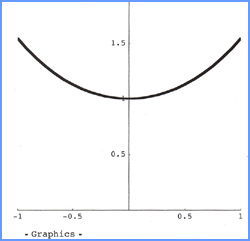
MATHEMATICA^®Code

The Catenary family of curves is easily entered and modified in MATHEMATICA® or on a graphing calculator.

There are additonal interesting properties. . . .

Certain functions containing e^x and e^-x occur sufficiently often in science and engineering to need a special name, hyperbolic functions. They are related to the equilateral hyperbola. Just as students learn to relate the trig functions to the unit circle, the hyperbolic functions have names related to the hyperbola as follows:

Hyperbolic sine of x:

Hyperbolic cosine of x:

Hyperbolic tangent of x:

Hyperbolic sine, cosine,
tangent equations

From Galileo's Dialogo on the Two New Sciences, 1638, published after his trial. He was 74 years of age and nearly blind when he wrote . . . .

On the Second Day, Salviati speaking:

"Drive two nails into a wall at a convenient height and at the same level; make the distance between these nails twice the width of the rectangle upon which it is desired to trace the semiparabola. Over these two nails hang a light chain of such length that the depth of its sag (curve or sacca) is equal to the length of the prism. This chain will assume the form of a parabola,* so that if this form be marked by points on the wall we shall have described a complete parabola which can be divided into two equal parts by drawing a vertical line through a point midway between the two nails. . . . Any ordinary mechanic will know how to do it."

Galileo Galilei, trans. by Henry Crew, 1950

* It is now well known that the "hanging chain" curve is not a parabola but our catenary. The equation of the catenary was first given 49 years after Galileo's death by James Bernoulli.

The name "catenary" is an Anglicized version of the Latin word catenaria first used by Christiaan Huygens in a letter sent to Gottfried Leibniz in 1690. Both words are derived from the Latin noun catena meaning "chain."

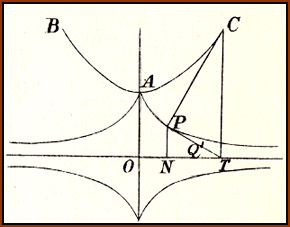
A Brief Historical Sketch . . .

Leonardo da Vinci sketched hanging chains in his notebooks.
Galileo mistook the shape to be that of a parabola.
Simon Stevin constructed problems dealing with hanging ropes.
René Descartes speculated on a letter from Isaac Beeckman:
Jungius disproved the shape to be a parabola (1669).
Huygens, Leibniz and John Bernoulli all replied to a challenge from Jacob Bernoulli posed in Acta Eruditorum to find the catenary's actual shape (1690-1691).
Jacob Bernoulli published their three solutions in Acta within months (June, 1691). See below.
David Gregory wrote a treatise on the catenary (1697).
Huygens proved to Mersenne that a hanging chain would not be a parabola.
Later, Leonhard Euler showed that a revolving catenary will generate the only minimal surface of revolution.

To underscore the historical importance of the catenary, we have selected the figures submitted by Gottfried Leibniz and Christiaan Huygens to Jacob Bernoulli for publication in the widely acclaimed Acta Eruditorum, 1691................................

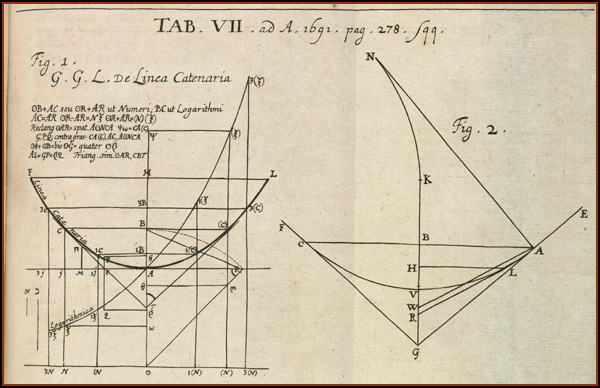Reproduced with permission from the Huntington Library, San Marino, California.
Leibniz's solution is on the left. Huygen's illustation is on the right.

And from another classic . . .

The perpendicular TP from the foot of the ordinate upon the tangent is of a constant length c, and therefore equal to OA, the perpendicular from the origin on the tangent at the vertex. The parameter of the curve is c in Carr’s proof.

The catenary was Proposition #5273 in George S. Carr's classic of classics, A Synopsis of Elementary Results in Pure Mathematics, 1886. This book guided British mathematics, especially in the highly competitive Mathematical Tripos at Cambridge for almost one-half century.

One of this books most ardent readers was Srinivasa Ramanujan who mastered its contents as a young man in India, and later, in his early 30s, read the book as a source of comfort when on his death bed.

And from another surprising source, a letter from Thomas Jefferson . . .

December 23, 1788
Paris, France

Thomas Jefferson, writing to another statesman, Thomas Paine,
regarding bridges to be built in his remote, young country:

". . .iron-men are much better judges than we theorists. - You hesitate between the catenary, and portion of a circle. I have lately received from Italy a treatise on the equilibrium of arches by the Abbé Mascheroni. It appears to be a very scientifical(sic) work. I have not yet had time to engage in it, but I find that the conclusions of his demonstrations are that 'every part of the Catenary is in perfect equilibrium.' . . .

To say another word of the Catenarian arch, without caring about mathematical demonstrations, it's nature proves to be in equilibrio in every point. It is the arch formed by a string fixed at both ends and swaying loose in all the intermediate points. . . .

I am with sentiments of sincere esteem & attachment, dear Sir, you friend and servant,
Th: Jefferson"

St. Louis Gateway Arch

The equation of the curve that approximates the Gateway Arch is
Equation for the Gateway
Arch

The Arch represents one of the largest optical illusions ever created. While it appears to be much taller than it is wide, the two distances are exactly the same at 630 feet.

Useful Links and Books

2015 Update: See Philosophical Transactions A - Celebrating 350 years of Philosophical Transactions: physical sciences papers (Theme issue edited by Dave Garner).
C. R. Calladine, An amateur's contribution to the design of Telford's Menai Suspension Bridge: a commentary on Gilbert (1826). On the mathematical theory of suspension bridges. Philosophical Transactions A, Vol. 373, Issue 2039, April 13, 2015, pp. 7-11.

http://www-history.mcs.st-and.ac.uk/history/Curves/Catenary.html

http://mathworld.wolfram.com/Catenary.html

Blackwell, Richard J. (trans.), Christiaan Huygens' The Pendulum Clock or Geometrical Demostrations Concerning the Motion of Pendula as Applied to Clocks, The Iowa State Univ. Press, 1986.

Boyd, Julian P., editor, The Papers of Thomas Jefferson, Princeton University Press, vol. 14, 1958, pp. 372-4.

Bukowski, John, Christiaan Huygens and the Problem of the Hanging Chain, The College Mathematics Journal, 39 (1), January, 2008.

Carr, George S., A Synopsis of Elementary Results in Pure Mathematics, London and Cambridge, 1886. The catenary was Proposition #5273 in this classic of classics that guided British mathematics, especially in the highly competitive Mathematical Tripos for one-half of a century.

One of the books most ardent readers was Srinivasa Ramanujan who mastered its contents as a young man in India, and later, in his early 30s, read the book as a source of comfort when on his death bed.

Galilei, Galileo, Two New Sciences - Including Centers of Gravity and Force of Percussion, trans. Stillman Drake, University of Wisconsin Press, 1974.

Galilei, Galileo, Dialogues Concerning Two New Sciences, trans. Henry Crew and Alfonso de Salvio, Northwestern Univ. Press, 1950.

Gray, Alfred, Modern Differential Geometry of Curves and Surfaces with MATHEMATICA^®, 2nd ed., CRC Press, 1998, pp. 55-57.

Lockwood, E. H., A Book of Curves, Cambridge University Press, 1961.

Swetz, Frank, John Fauvel, Otto Bekken, Bengt Johansson and Victor Katz, Learn from the MASTERS!, MAA, 1995, pp.123-130.
(See V. Frederick Rickey, "My Favorite Ways of Using History in Teaching Calculus", in Swetz, et al.)

Ventress, Andy, "Digital Images+Interactive Software=Enjoyable, Real Mathematics Modeling," Mathematics Teacher, 101 (8), April 2008, pp. 568-572.

Yates, Robert, CURVES AND THEIR PROPERTIES, The National Council of Teachers of Mathematics, 1952.