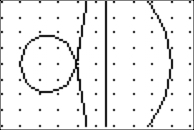
|
For
the Conchoid
of Nicomedes....
 |
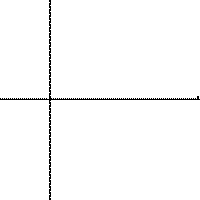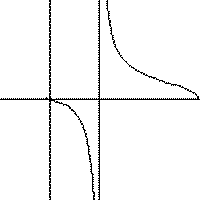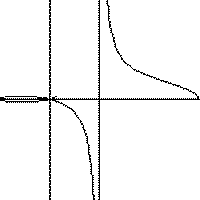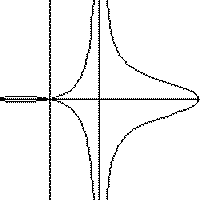
Replay the animation |
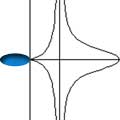
Definition: Let S be any curve and let A
be a fixed point. If a straight line is drawn
through A to meet
the
curve at Q, and if P and P' are points on this line
such that PQ = P'Q
=
a constant term, the locus of the points P and P' is
called a conchoid
of
the curve with respect to the fixed point A.
|
|
MATHEMATICA®Code
 The Conchoid family of curves is easily entered and modified on a graphing calculator. Be sure to use (1/cos) for the secant term. |
|
Historical Sketch Nicomedes (ca. 225 BC) is credited with being the
first
to investigate the conchoid, a name from the
Greek meaning
"shell-like" or "shell form." He sought to find
two mean
proportions between
given lengths in order to solve the famous Delian
problem. The Delian problem is also known as duplication of
the
cube;
in other words, finding the edge of a cube having a
volume exactly
twice
that of a given cube. This is one of the three
famous
constructions
dating from antiquity. If, contrary to Euclidean
assumptions, we
permit ourselves to mark a straight edge, the conchoid
may, in fact be
applied to these famous problems. With adjustments in various constant terms, the
conchoid
is modified into a circle, spiral, limaçon, or
cardiod.
Moreover, we find equations for the conchleoid
and conchal as
well as focal conchoids of conic sections in the
literature. But
the most famous are the . . . . . .
To underscore the historical importance of the
conchoid,
we have selected Figure #139 of John Colson's
translation of Maria
Gaetana Agnesi's Instituzioni analitche, now
generally
recognized as the first book of mathematics written by
a woman.
Colson held the prestigious Lucasian chair
at
Cambridge. In 1801 he chose to translate
Agnesi's widely
acclaimed treatise on Calculus written one-half
century earlier (1748).
Unfortunately, his translation of the name of the
curve now known in
English speaking countries as the Witch of Agnesi
was a
slight, but lasting error. However, his Conchoid
of Nicomedes
was accurate and an indication of the enduring fame of
this popular
curve. Colson's EXAMPLE IV speaks for
itself.  Reproduced
with
permission from the Rare Books Division, Dept. of
Rare Books and
Special
Collections, Princeton University Library.
Please observe
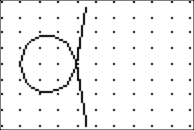
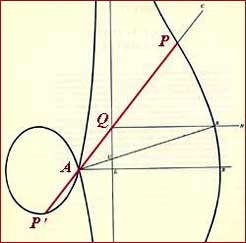
that
Agnesi first sketched a circle to generate
both her Witch
and the conchoid
before proceeding to give
a proof.
|
||||||||||
|
|
| http://www-history.mcs.st-and.ac.uk/history/Curves/Conchoid.html |
| http://mathworld.wolfram.com/ConchoidCurve.html |
| Eves, Howard, An Introduction
to the History of Mathematics, 6th ed,. The
Saunders College
Publishing, 1990. |
| Gray, Alfred, Modern Differential Geometry of Curves and Surfaces with MATHEMATICA®, 2nd ed., CRC Press, 1998, p. 898. |
| Lockwood, E. H., A Book of
Curves, Cambridge University Press, 1961. |
| Shikin, Eugene V., Handbook
and
Atlas of Curves, CRC Press, 1995. |
| Yates, Robert, CURVES AND
THEIR PROPERTIES, The National Council of Teachers of Mathematics,
1952. |
|
Gustavo Gordillo, 2006. |