Click on the thumbnail
images below to
see
experimental solar
collectors
near Barstow,
California
focus the sun's rays on
a central
tower
where heat
is converted to
electricity.



The famous Belvedere Apollo at the top
of this column is a Roman copy
of a much older Greek statue.
This marble is now in the
Pio Clementino Museum
at the Vatican (Rome, Italy).
The Burning Mirrows wall painting is from the
Stanzino
delle Matematiche
in the Galleria degli Uffizi (Florence, Italy).
Painted by Giulio
Parigi
(1571-1635) in the years 1599-1600.
|
This section . . .
Another attempt
to solve one of the three famous construction
problems from Antiquity.
Biographical
Sketch
Diocles
is one of many mathematicians who have attempted
to construct a cube whose volume is exactly twice
that of a given cube. This is often called
the "Delian" problem or "duplication of the cube".
Legend:
A
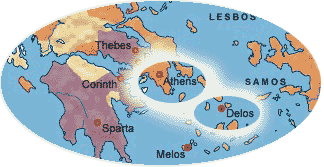
number of legends surround this construction
challenge. The good citizens of Athens were
being devastated by a plague. History
records that in 430 BC they sought advice from the
oracle at Delos on how to rid their community of
this pestilence. The oracle replied that the
altar of Apollo, which was in the form of a cube,
should be doubled. Thoughtless builders
merely doubled the edges of the cube.
Unfortunately the volume of the altar increased by
a factor of 8.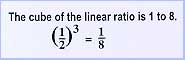 The oracle insisted the
gods had been angered. As if to confirm this
reprimand, the plague grew worse. Other
delegations consulted Plato. When informed
of the oracle's admonition, Plato told the
citizens "the god has given this oracle, not
because he wanted an altar of double the size, but
because he wished in setting this task before
them, to reproach the Greeks for their neglect of
mathematics and their contempt of geometry." The oracle insisted the
gods had been angered. As if to confirm this
reprimand, the plague grew worse. Other
delegations consulted Plato. When informed
of the oracle's admonition, Plato told the
citizens "the god has given this oracle, not
because he wanted an altar of double the size, but
because he wished in setting this task before
them, to reproach the Greeks for their neglect of
mathematics and their contempt of geometry."
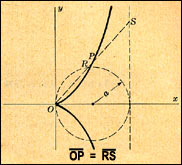
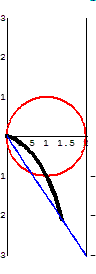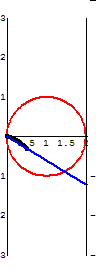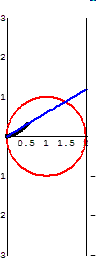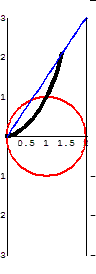
The
curve invented by Diocles in about 180 BC later
appears in the works of Fermat, Roberval, Huygens,
Wallis, Newton, and others. Problems on the
cissoid's curvature, arc length, and areas bounded
by its asymptote are found in modern calculus
texts.
The
cissoid also has much in common with the modern
need to identify the focal point of a satellite
"dish." The cissoid may be represented as
the "Roulette for the Vertex of a Parabola", or
the curve traced by a fixed point on a parabolic
curve as that curve rolls without slipping along a
second curve. Thus, if a fixed point on a
parabola moves along a second parabola of similar
dimensions, the vertex will become the cusp of a
cissoid of Diocles. Moreover, if the cusp is
taken as the inversion center, the cissoid inverts
to a parabola.
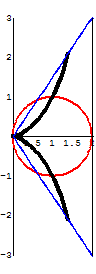
 Diocles investigated the
properties of the focal point of a parabola in On
Burning Mirrors. There is a similar
title in the works of Archimedes. The
problem, then as now, is to find a mirror surface
such that when it is placed facing the sun, heat
is produced. Legend suggests Archimedes
wanted to use parabolic mirrors reflecting the
sun's rays to burn the sails of enemy ships. Diocles investigated the
properties of the focal point of a parabola in On
Burning Mirrors. There is a similar
title in the works of Archimedes. The
problem, then as now, is to find a mirror surface
such that when it is placed facing the sun, heat
is produced. Legend suggests Archimedes
wanted to use parabolic mirrors reflecting the
sun's rays to burn the sails of enemy ships.
Today,
experimental solar collectors near Barstow,
California, focus the sun's rays on a central
water tower where heat is converted to
electricity.
| A Brief Listing of
references
that should
be in most university libraries.
Boyer, Carl B.
A
History of Mathematics,
various editions and publishers.
Katz, Victor
J. A
History of Mathematics,
2nd ed., Addison-Wesley, 1998.
Toomer,
Gerald. Diocles
on Burning
Mirrors, Springer, 1976.
The History of
Mathematics:
A Reader.
Edited by John Fauvel
and Jeremy
Gray,
Macmillan and The
Open University,
1987, pp.
181-182.
|

Plato
|
|







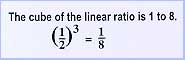 The oracle insisted the
gods had been angered. As if to confirm this
reprimand, the plague grew worse. Other
delegations consulted Plato. When informed
of the oracle's admonition, Plato told the
citizens "the god has given this oracle, not
because he wanted an altar of double the size, but
because he wished in setting this task before
them, to reproach the Greeks for their neglect of
mathematics and their contempt of geometry."
The oracle insisted the
gods had been angered. As if to confirm this
reprimand, the plague grew worse. Other
delegations consulted Plato. When informed
of the oracle's admonition, Plato told the
citizens "the god has given this oracle, not
because he wanted an altar of double the size, but
because he wished in setting this task before
them, to reproach the Greeks for their neglect of
mathematics and their contempt of geometry."
 Diocles investigated the
properties of the focal point of a parabola in On
Burning Mirrors. There is a similar
title in the works of Archimedes. The
problem, then as now, is to find a mirror surface
such that when it is placed facing the sun, heat
is produced. Legend suggests Archimedes
wanted to use parabolic mirrors reflecting the
sun's rays to burn the sails of enemy ships.
Diocles investigated the
properties of the focal point of a parabola in On
Burning Mirrors. There is a similar
title in the works of Archimedes. The
problem, then as now, is to find a mirror surface
such that when it is placed facing the sun, heat
is produced. Legend suggests Archimedes
wanted to use parabolic mirrors reflecting the
sun's rays to burn the sails of enemy ships.