Anton, Howard and
Rorres,
Chris, Elementary
Linear
Algebra, Wiley, 2010, pp. 112-113.
|
Brown, B. H., La
Courve du diable, The American Mathematical Monthly,
vol. 33 (5) May,1926, pp. 273-274.
|
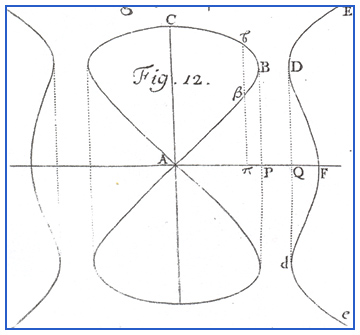
Cramer, Gabriel, Introduction à
l'analyse des lignes
courbes algébriques, Genève, Chez les
Frères
Cramer & Philibert, 1750.
|
Fladt, Kuno, Analytische
Geometrie spezieller ebener
Kurven, Akademische Verlagsgesellschaft,
1962, p. 218.
Fladt uses "Die Teufelskcurve
von Gabriel
Cramer." Teufelskcurve
may be translated as either the Devil's Curve or
the Devil's hairpen.
|
Gray, Alfred, Modern Differential
Geometry of Curves
and Surfaces with MATHEMATICA®, CRC Press, 1998,
p. 92.
|
Lacroix, Silvestre
François, Traité
du
calcul différentiel et du calcul intégral, vol.
1,
Libraire pour les Mathématique, quaai des
Augustins, 1797.
|
Koestler, Arthur, The SLEEPWALKERS,
Arkana: Penguin
Books, 1989.
|
Rider, Paul R., The
Devil's Curve and
Abelian Integrals, The American
Mathematical Monthly, vol. 34 (4)
April, 1927, pp. 199-203.
|
| Stewart,
James, Calculus:
Early Transcendentals,
7th ed., Cengage: Brooks/Cole, 2012, p. 215. |
Venit, Stewart and
Bishop,
Wayne, Elementary
Linear Algebra,
4th ed., ITP Publishing Co., 1996, pp.
183-184. Proof: pp.
187-188.
ISBN:
053495190-2 |
Weisstein, Eric., Devil's Curve,
< http://mathworld.wolfram.com/DevilsCurve.html
>.
Weisstein, Eric, CRC Concise
Encyclopedia of Mathematics, CRC Press,
1999, pp. 424 - 425.
|
Yates, Robert C., Curves and their
Properties,
NCTM, 1974, p. 203. Yates writes, "This
curve is found useful in
presenting the theory of Riemann surfaces and
Abelian integrals."
Yates' reference to Brown's publication is
invaluable.
|
|