| According to Harry F. Davis, writing in 1961, the Coriolis acceleration is "more complicated and is usually not discussed in elementary physics textbooks." He suggests a careful examination of the derivation will show the term applies "partly to the change in direction of the radial component of velocity, and partly to the fact that, as the radius changes, the transverse component of velocity changes, even if the angular velocity is constant." Professor Davis did not have the advantage of computer animation. Tevian Dray has used the surface of the earth to illustrate this phenomenon. Moreover, modern calculus texts with a chapter on "Vector Functions" covering planetary motion may have problems on this subject. |
References
Harry F. Davis, Introduction to Vector Analysis, Allyn and Bacon, Inc. 1961. James Stewart, Calculus, 5th ed., THOMSON Brooks/Cole, 2003. |
|
|
| For other animations showing that
rotations do not necessarily commute, see < http://www.physics.orst.edu/~tevian/Rotations/RotXY.gif > < http://www.physics.orst.edu/~tevian/Rotations/RotYX.gif >. |
| Windpower and the Coriolis effect < http://www.windpower.org/en/tour/wres/coriolis.htm >. |
| For a biography of Coriolis, see < http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Coriolis.html >. |
| For the Vector Calculus Bridge Project, see < http://www.physics.orst.edu/bridge>. |
| For the Paradigms in Physics
Project ( NSF DUE
Project #9653250 ), see < http://www.physics.orst.edu/paradigms>. The Earth Hockey animations were developed as part of the Paradigms Project. |
| For more information, please
see David McIntyre's article in American Journal
of Physics, 68,1097-1105 (2000).
Type "Coriolis" in the "Keyword Quick Search." McIntyre created these animations using Mathematica®. In addition, we recommend visiting his web site < http://www.physics.orst.edu/~mcintyre/coriolis >. |
 |
Tevian
Dray presented the Vector Calculus Bridge Project
at MathFest 2003. His minicourse emphasized
vectors and vector calculus.
In the program he wrote, "The key to bridging the gap between mathematics and the physical sciences is geometric reasoning." This approach was pioneered by the French mathematician Gaspard Gustave de Coriolis (1792 - 1843). He showed that the laws of motion could be used in a rotating system if an extra force, now called the Coriolis acceleration, is added to the equations of motion. In 1835 Coriolis wrote on a mathematical theory of billiards. Similarly, Dray has chosen to call his investigations "earth hockey." |
 |

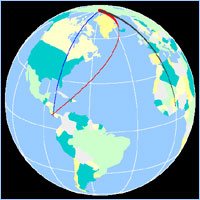
 Coriolis acceleration is the
apparent acceleration one sees when observing
particle motion from a rotating, rather an an
inertial, reference frame. For instance,
the needle of a phonograph moves (nearly) in a
straight line, yet traces a spiral on the
rotating record.
Coriolis acceleration is the
apparent acceleration one sees when observing
particle motion from a rotating, rather an an
inertial, reference frame. For instance,
the needle of a phonograph moves (nearly) in a
straight line, yet traces a spiral on the
rotating record. 