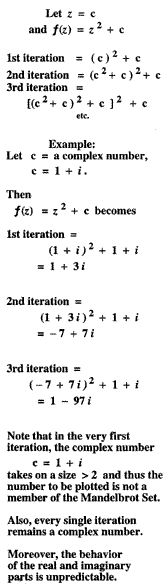| Mathematicians
in the early 20th century investigated curves
that had highly intricate and detailed
shapes. Moreover, they realized that
while a region might be bounded and thus the
area finite, the perimeter or border might
seem to be infinite. These curves - the
Koch Snowflake for example - with finite area
and infinite perimeter, were given the name of
"pathological." This particular area of
research in mathematics has generated colorful
names: Cantor's dust, Polya's sweeps, Peano's
dragons, Sierpinski's carpet and others.
When the
edge of a curve under many iterations is
broken, repeated, scaled down, and then
scaled down again as the iterations
progress, the curve has now become known as
a fractal. This relatively new word in
mathematics was first coined by Benoit B.
Mandelbrot and introduced to mathematicians
and computer scientists in The Fractal
Geometry of Nature published in
1983. He suggested the coastline of
Great Britain, with its capes within capes,
and bays within bays, surrounding a known
land mass, be the mental model.
Librarians noted the August, 1985 article in
Scientific American on the "new
fractal geometry" was extremely popular.
Other
writers have suggested the viewer look at a
curve and then zoom in for a closer
look. Like Sherlock Holmes, with a
magnifying glass, the viewer must
search. He does not know where on the
curve he views. Curves within
curves. Patterns within
patterns. Iterations within
iterations.......The same repetitious but
scaled pattern appear in a true
fractal. The area is bounded, but the
perimeter seems to be infinite.
Technology
made this formerly tedious mathematics
possible. With the help of the
computer in the 1960s, Mandelbrot returned
to earlier research questions first posed
between 1915 and 1930 by French
mathematicians Gaston Julia and Pierre
Fatou: "Does the iteration of a function
drive the result off to infinity or does the
result approach and remain close to some
well-defined value?" With recursion no
longer difficult, a mathematician could
write a program and then simply wait, with
great curiosity, for the speed of the
computer to provide some answers.
In addition
to Mandelbrot, John Hubbard of Cornell
University and Adrian Douady of the Ecole
Normale Superieure, Paris, and P. T.
Bierberg of Finland are credited with acute
observations, research, and early
publications.
|