Golden Ratio
More members of the
Spiral Family of Plane Curves:
The Spirals of
Archimedes, of Fermat, of Euler, of
Cornu,
- Hyperbolic,
Logarithmic, Spherical, Parabolic,
Nielsen's, Seiffert . . . .
|
Click here for the full
article.
|
We are
familiar with the concept of
gnomonic tiling in which a figure
added to another reproduces the
shape of the original. The process
can repeated over and over to form
a tessellated mosaic that covers
the plane. The initial tile is
called the seed and the added
piece is called the gnomon. The
gnomon generally increases in size
geometrically, i.e., by a power
law. Figures thus created are
called whorled figures, as the
gnomons are usually added in a
circular fashion about the seed.
See, for example, Gazalé [1] and
Waldman [2].
|
|
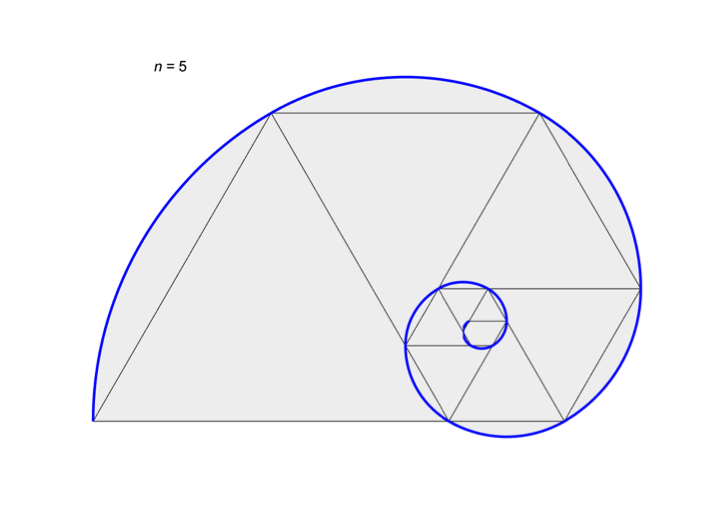
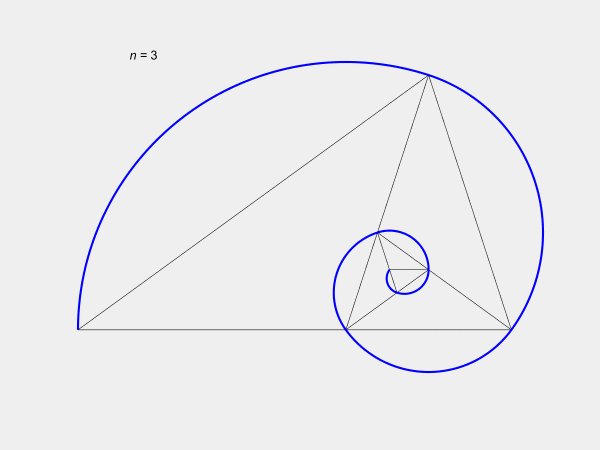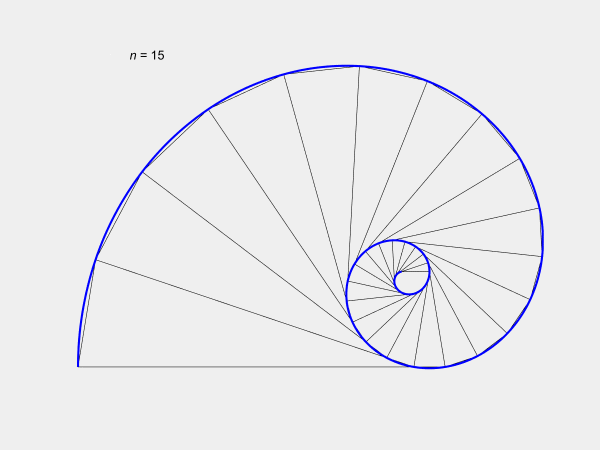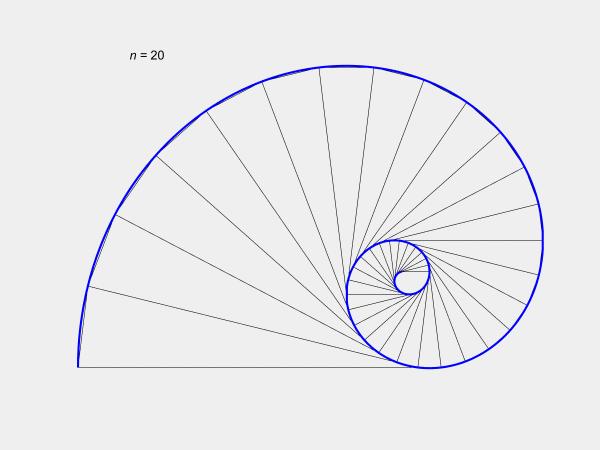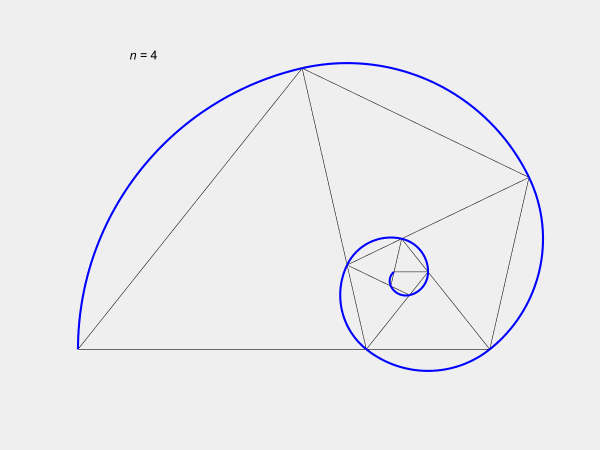
Our Figure 1
shows a whorled plastic pentagon.
|
There are
magnificent mosaics, or tilings, if
you prefer, that continue to amaze
us. These are the whorled plastic
pentagon, with its equilateral
triangle gnomon, and the whorled
golden rectangle, with its square
gnomon, shown in Figure 1 and Figure
2, respectively. The former has a
growth rate of p, the plastic
number, and the later has a growth
rate of , the golden ratio.
|
|
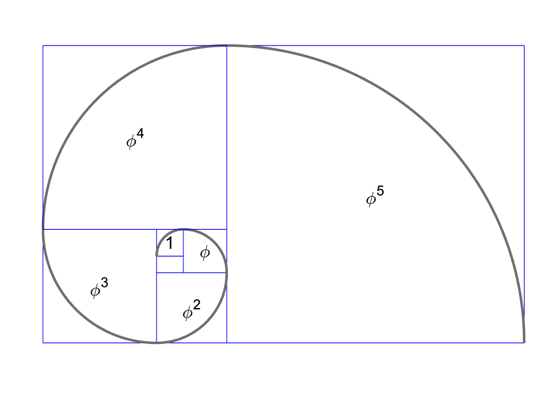
Figure 2: Golden rectangle and
its square gnomon with a growth
rate of the Golden Ratio.
It’s fairly
well established that the
whorled figures in Figure 1 and
Figure 2 are the only ones whose
gnomons are regular polygons, by
which we mean, of uniform sides
and internal angles.
Insofar
as
we have developed a program
for creating pseudospirals and
their attendant triangles (or
squares), we wondered if we
could find additional mosaics
that covered the plane.
. . . . . . . . . . . . . .
|
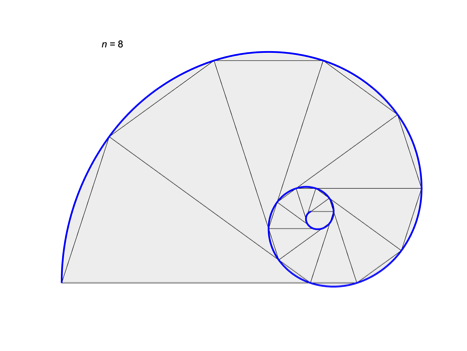Figure
3: An octagon and its golden
triangle gnomon.
Voilà! We
found by experimentation the
pseudospirals with a sequence
and rotation angle produce a
whorled octagon with
an isosceles triangle
gnomon. The growth rate q
was determined empirically. The
result is shown in Figure 3.
Interestingly, the gnomon is the
golden triangle.
This
set the stage for us to (a)
determine the growth rate
analytically, and (b) see if the
result could be generalized for
other growth rate and turn
angles. The
technical details and
nomenclature that followed are
included in the attached pdf
file.
|
|
|
2017