Goodstein's Theorem

Instructions:

Pick a number - a positive integer - expressed in simple base notation.
Then repeatedly - recursively - perform the following two operations:

Subtract one from the number.

Increment the base.

What will happen? The answer is the number eventually converges to 0. Most people incorrectly guess the sequence goes to infinity. Let's begin by studying this recursion in simple base notation.

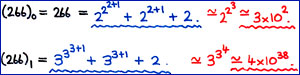
For number = 4 and base = 2,

Start.

[1, 0, 0] (base 2) = 4

[1, 1] (base 3) = 4
Completed 1 iteration.

[1, 0] (base 4) = 4
Completed 2 iterations.

[3] (base 5) = 3
Completed 3 iterations.

[2] (base 6) = 2
Completed 4 iterations.

[1] (base 7) = 1
Completed 5 iterations.

[0] (base 8) = 0
Completed 6 iterations.

For number = 3 and base = 2,

Start.

[1, 1] (base 2) = 3

[1, 0] (base 3) = 3
Completed 1 iteration.

[2] (base 4) = 2
Completed 2 iterations.

[1] (base 5) = 1
Completed 3 iterations.

[0] (base 6) = 0
Completed 4 iterations.

For number = 5 and base = 3,

Start.

[1, 2] (base 3) = 5

[1, 1] (base 4) = 5
Completed 1 iteration.

[1, 0] (base 5) = 5
Completed 2 iterations.

[4] (base 6) = 4
Completed 3 iterations.

[3] (base 7) = 3
Completed 4 iterations.

[2] (base 8) = 2
Completed 5 iterations.

[1] (base 9) = 1
Completed 6 iterations.

[0] (base 10) = 0
Completed 7 iterations.

For number = 10 and base = 8,

Start.

[1, 2] (base 8) = 10
[1, 1] (base 9) = 10
Completed 1 iteration.
[1, 0] (base 10) = 10
Completed 2 iterations.
[9] (base 11) = 9
Completed 3 iterations.
[8] (base 12) = 8
Completed 4 iterations.
[7] (base 13) = 7
Completed 5 iterations.
[6] (base 14) = 6
Completed 6 iterations.
[5] (base 15) = 5
Completed 7 iterations.
[4] (base 16) = 4
Completed 8 iterations.
[3] (base 17) = 3
Completed 9 iterations.
[2] (base 18) = 2
Completed 10 iterations.
[1] (base 19) = 1
Completed 11 iterations.
[0] (base 20) = 0
Completed 12 iterations.

Now that you have examined simple base notation, you are ready to tackle Goodstein's Sequence, which uses hereditary base notation. Amazingly, Goodstein's Sequence also converges to 0!

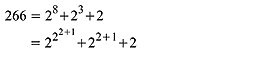
Equation

If base two is recursively incremented to base three, the right side of the expression becomes

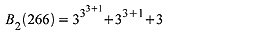
Equation

The Goodstein Sequence is therefore

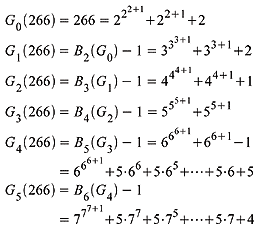
Equation

The following applet is written in the Goodstein hereditary base notation. Enter a number, its base, and then select "Start." If you select a number greater than 3 base two, the recursion can take a long time to converge and requires your computer to have sizable memory. [Note: We suggest you begin with 3 base two; and then try 4 base three. After these two examples that converge quickly, try other larger numbers. Please observe that if the base is larger than the number, the sequence converges quickly. Even numbers as small as 4 base two can increase for approximately 2.6 × 10^60605351 steps]. The program will terminate if the number becomes to large.

value: base:

If you enjoy writing applets, please be sure to look at the source code.

For the more advanced student. . . . On Proof and Goodstein's Theorem

Goodstein's statement about natural numbers cannot be proved using only Peano's arithmetic and axioms. Goodstein's Theorem is proved in the stronger axiomatic system of set theory by applying Gödel's Incompleteness Theorem.

The Incompleteness Theorem asserts that powerful formal systems will always be incomplete. That is to say, there will exist true statements that the system cannot prove nor disprove. Gödel's Incompleteness Theorem assures us that we must believe Goodstein's theorem even if it cannot be proved by mathematical induction.

The crucial insight for Goodstein's sequence is that the iterations are well-ordered. In our examples, note that the order of the iteration counted backwards, always goes to zero.

Interestingly, the Goodstein sequence is unique in that it may calculate large numbers before the size of the base forces the sequence to converge to zero. The calculation for larger numbers reaches a point where the computer may be unable to continue. Many personal computers will simply cease the calculation.

References

Goodstein, R. L. "On the Restricted Ordinal Theorem." J. Symb. Logic 9, 33-41, 1944.

Henle, J. M. An Outline of Set Theory, Springer-Verlag, 45 - 48, 1986.

For On-line seminar notes:
< http://www2.maths.bris.ac.uk/~maadb/research/seminars/online/fgfut/ >

"Although no naturally occurring dynamical systems are known to exhibit the behavior of a Goodstein Sequence, the Goodstein dynamical system is of interest because its properties greatly differ from the common strange-attractor systems." Justin T. Miller, University of Arizona
http://www.u.arizona.edu/~miller/thesis/node3.html

For examples of a Goodstein Sequence in hereditary notation equations

http://en2.wikipedia.org/wiki/Goodstein's_theorem

For students interested in mathematical proof:
http://astronomy.swin.edu.au/~pbourke/analysis/goodstein/

For an encyclopedia of integer sequences:
http://www.research.att.com/~njas/sequences

Related
Topics

Hereditary Sequences
Peano's axioms and arithmetic
Gödel's Incompleteness Theorem
"Well-ordered" in proof

Reuben Goodstein (1912 - 1985)
was a student of Littlewood's at Cambridge.
See "Hardy and Littlewood."

R. L. Goodstein

Dr. Russell Abbott, 2004
Matthew Nelson, FITSC Lab, CSULA, 2004
Jonathan Sahagun, 2018