|
|
|
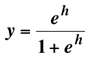
This is an example of
logistic regression,
a continuous
function. However,
note
that a rectangle could be
drawn under
any one of the jumps in
the curve.
When the pixels are
smoothed
to represent continuous
data,
the graph is named an ogive curve.
When
the second derivative is
zero, the slope is zero,
and we have a "point of
inflection."
Segment
at the point of
inflection.
Note:
Study
the graphing
calculator
image. Notice
the graph is not
smooth and
continuous. It
is conventional to
define the cumulative
frequency for all
values of x up to and
including the given
right end-point
value. Thus, an
ordinate
represents the sum of
all frequencies up to
and including a
corresponding
frequency in a
frequency
distribution.
Your calculator or
software will
calculate a value of y to be
mapped with the
corresponding value of
x but
must "jump" to
represent a continuous
function.
|
|
|
|
In mathematics, the
name ogive
is applied to any continuous
cumulative frequency polygon and is
derived from its resemblance to the
shape of architectural molding known
as the ogee pattern.
Another way to express this is to
say an ogive curve has the shape of
an elongated S. Also,
it is sometimes called a "double
curve" with one portion being
concave and the other being convex.
|
Be careful in drawing
a distinction between ogive
and ogee,
especially when applied to
architecture. Conflict abounds
in the literature and common usage.
For example, a 1954 edition of the
Funk and Wagnalls dictionary uses the
term ogive to describe
the arch over doorways and windows as
illustrated by the north entrance to
Westminster Cathedral, London.
"This sense is wholly arbitrary and is
unknown before 1830, when it appears
to have been adopted through a
misunderstanding, but it is of
frequent occurrence since that date."
A mathematician viewing the ogive
pattern as seen in the window notes a
cusp at the apex. The slope is
undefined at the point of a cusp.
The same dictionary defines ogee
as
a "cyma reverse molding" and having a
"section in reverse" or as a
"long S curve" and
continues by using the examples
of "ogee doorway" and "ogee window."
|

|
|
Proud
owners of early American mantle
clocks use the term ogee
to describe a weight-driven pendulum
mechanism in a rectangular
case. The owners know the
internal weight on the left must be
wound in a clockwise direction while
the weight on the right is hoisted
using a counterclockwise direction,
thereby aping the pattern of arches
in cathedrals.
(The Smithsonian
Institution is on the middle panel.)
|

|
|
Other
Examples
|
The Instituto
Veneto di Scienze, Lettere ed Arti in
Venice.

The ogive
curve is sometimes called the
"Venetian Arch."
|
Another early
American clock
with an "ogee" mechanism and an
"ogive" case.

|
|
|
|
Classic
Birthday Problem ~ An Ogive Curve
What is
the probability that at least two
people in a given group will have the
same birthday?
For this problem we ignore leap years
and assume that a person's birthday
can fall on any day with the same
probability.
Numerator:
If
the n persons are
to have different birthdays, the the
first person can be born on any of the
365 days, but the second person can
only be born on one of the remaining
364, the third person on the remaining
363 days, etc.
Denominator: As there are
n
people
and 365 different days, there are 365 n
possible ways in which the people
might have their birthdays.
For a group as small as 23 people, the
probability becomes less than
one-half, or less than "50-50" that
two people will not have the same
birthday. In other words, it is
more likely to find that two people
will have the same birthday.
|
|
References
| For
those who have
MATHEMATICA®, . . .Alfred
Gray, Modern Differential
Geometry, 2nd ed., CRC
Press, 1998, p. 909 has logistic
code. |

|
|
J. F. Kenney and E.
S. Keeping, Mathematics
of Statistics: Part One,
D. Van Nostrand Co., 1954, pp. 29-31.
|
| Eric W. Weisstein, CRC
Concise Encyclopedia of Mathematics,
CRC Press, 1999, p. 1267. |
|
|

