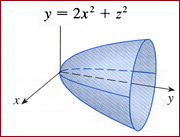
The Paraboloid and Elliptical Paraboloid

Instructions:

This interactive animation requires three downloads. First, your computer must have Java and Java 3D. Then you must download the JAR file to your desktop. Please note that the Java3D software is only available for Windows and Solaris.

For download assistance click here. This takes patience.

____

Having now downloaded both Java and Java 3D, you may run the animation for the Paraboloid on the right by downloading the following:

Animation Download

After the download, simply double click on the JAR file to see the interactive animation.

Tech savy programmers may enjoy the following source code:

Animation Source Code

Background for the student. . . .

Significance of Quadric Surfaces

Three-dimensional analogs of the conic sections are an important class of surfaces studied in Calculus.

Elliptic Paraboloid The trace, or cross section, in the xy-plane is a point. If c= 1, the point is the origin (0,0). The traces in planes parallel to and above the xy-plane are ellipses. The traces in the yz-plane and xz-plane are parabolas, as are the traces in planes parallel to these. In this example

Horizontal traces are ellipses.
Vertical traces are parabolas.
The variable raised to the first power indicates the axis of the paraboloid.

If a = b and both are greater than 0, the horizontal traces are circles. The surface is then simply named a paraboloid or circular paraboloid.

General Equation

By translation and rotation the cross-product terms disappear and one of two standard equations will be

for all quadrics. These may include the ellipsoid and a wide variety of hyperboloids.

Volume of a Circular Paraboloid

Another example:

Note that y in the equation has only the first power and becomes the axis of the elliptical paraboloid.

Printed References

Modern calculus texts will have extensive material on the quadric surfaces. The student should be very attentive to instruction on learning graphing techniques.

For Mathematica® code that will create many variations of these graphs see
Gray, A., MODERN DIFFERENTIAL GEOMETRY of Curves and Surfaces with Mathematica®, 2nd. ed., CRC Press, 1998.

Gray, A., "The Paraboloid" in Modern Differential Geometry of Curves and Surfaces, CRC Press, 1993.

Applications

Home satellite dish
Radiotelescope
Reflecting telescope
Communication networks

Warning:

This animation requires three downloads. First, your computer must have Java and Java 3D. Then you must download the JAR file to your desktop. Please note that the Java3D software is only available for Windows and Solaris. Installation will take several minutes.

Java Software

If you do not have the free Java software, go to http://www.java.com/ and click on "Get It Now." Follow the on-screen instructions to download and install all components.
Now that you have the Java software, go to http://java.sun.com/products/java-media/3D/download.html to also download Java 3D.

Click on the Download button for Java 3D Software.
Accept the terms of the License Agreement.
Select the Java 3D Runtime for the JRE appropriate for your computer.
Once the download is complete, run the executable file to install.

Now you're ready to run this animation of the Möbius Strip.

November 6, 2003

Dr. Russell Abbott
Students of CS 390, Summer, 2003
Matthew Nelson, FITSC Lab, CSULA