|
In each of the pictures below, x is the
horizontal dimension
(width), y is
the vertical
dimension (height), and z is the
color (depth). To
more clearly show the contours of the z
surface, the color has been quantized (summarized)
into 16 distinct
levels:
| 0
= BLACK |
1
= BROWN |
2
= RED-BROWN |
3
= RED |
| 4
= ORANGE |
5
= YELLOW-ORANGE |
6
= YELLOW |
7
= YELLOW-GREEN |
| 8
= GREEN |
9
= CYAN |
10
= BLUE |
11
= INDIGO |
| 12
= VIOLET |
13
= BLUE-GREY |
14
= GREY |
15
= WHITE |
The drawing program
plots
thin black lines to represent the x
and y axes,
and a thin white
line to show where the 3-dimensional surface crosses
the z=0
plane. You can click
on any picture on this page to
see a full-screen version that you can study in
detail.
|
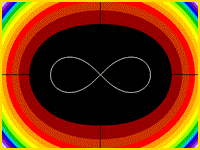
Circle
r = cos(q)
z = x/r - r
Drawing Limits: (-2, -2) - (2, 2)
Min z: -3.3, Max z: 0.993744
|
|
Cardioid
r = 1 + cos(q)
z = 1 + x/r - r
Drawing Limits: (-2, -2) - (2, 2)
Min z: -2.3, Max z: 1.99374
|

|
Pascal's Rose
r2 = cos2(2q)
z = (x4 - 2x2y2
+ y4)/r4
- r2
Drawing Limits: (-2, -2) - (2, 2)
Min z: -6.176, Max z: 0.99996
|
 |
Three Leaf Limaçon
r = cos(3q)
z = (4x3/r3 - 3x/r) - r
Drawing Limits: (-2, -2) - (2, 2)
Min z: -3, Max z: 0.993743
|

|
Daisy
r2 = cos2(4q)
z = ((x8 - 12x6y2
+ 38x4y4
- 12x2y6 + y8)
/ r8) - r2
Drawing Limits: (-2, -2) - (2, 2)
Min z: -5.53901, Max z: 0.999956
|

|
Checkerboard
z = cos(x) + cos(y)
Drawing Limits: (-10, -10) - (10, 10)
Min z: -1.99981, Max z: 2
|
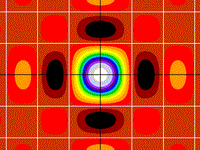 |
Two Dimensional Sampling Function
z = (sin(x)/x)(sin(y)/y)
Drawing Limits: (-10, -10) - (10, 10)
Min z: -0.217229, Max z: 1
|
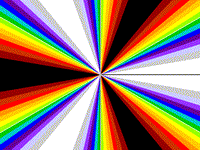 |
Rays
z = cos(3q)
z = 4x3/r3 - 3x/r
Drawing Limits: (-10, -10) - (10, 10)
Min z: -1, Max z: 1
|
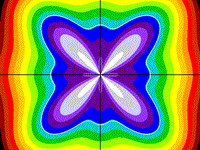 |
Four Petal Daisy
r2 = cos2(4q), with
odd lobes suppressed
z = x/r - r
Drawing Limits: (-2, -2) - (2, 2)
Min z: -3.3, Max z: 0.993744
|
 |
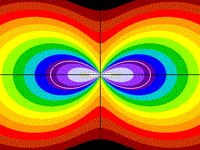
Six Leaf Clover
r2 = cos2(3q)
z = 16x6/r6 - 24x4/r4
+ 9x2/r2
- r2
Drawing Limits: (-2, -2) - (2, 2)
Min z: -6.1261, Max z: 0.993755
|
 |
Two Petal Rose
r = cos(2q)
z = ((x2 - y2) / r2)
- r
Drawing Limits: (-2, -2) - (2, 2)
Min z: -3.3, Max z: 0.993744
|
|
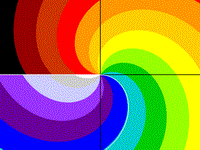
Spiral
r = q
z = tan-1(y/x) - r
Drawing Limits: (-2, -2) - (2, 2)
Min z: -5.13848, Max z: 3.13479
|
|
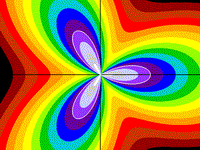
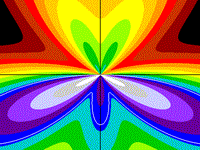
Butterfly
basically, r = versin(5q)
with lobe sizes
adjusted
z = ((4y5 - 4y3x2
+ 8yx4) /
r5) - (3y3 - 3yx2)/r3
- r
Drawing Limits: (-2, -2) - (2, 2)
Min z: -5.11643, Max z: 2.86601
|
|
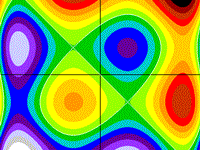
Circus Tent
a pair of polynomials with 5 roots each
z = x5 - 5x3 + 4x - y5
+ 5y3
- 4y
Drawing Limits: (-2, -2) - (2, 2)
Min z: -6.91267, Max z: 6.88453
|
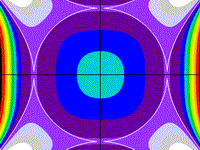 |
Two Hyperbolae and a Circle
z = (x2 - y2 - 1) (y2
- x2
- 1) (x2 + y2 - 1)
Drawing Limits: (-1.5, -1.5) - (1.5, 1.5)
Min z: -5.07812, Max z: 1.67009
|
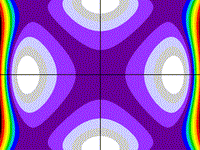 |
Radial Hyperbolae and Circle
r2 = (x2 - y2
- 1) (y2 - x2
- 1) (x2 + y2 - 1)
z = (x2 - y2 - 1) (y2
- x2
- 1) (x2 + y2 - 1) - r2
Drawing Limits: (-1.1, -1.1) - (1.1, 1.1)
Min z: -1.42419, Max z: -0.851859
|
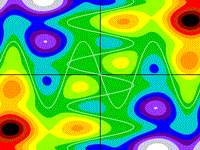 |
Intersecting Waves
basically, y = sin(3x) and x = sin(5y)
z = (sin(3x) - y) (sin(5y) - x)
Drawing Limits: (-3, -3) - (3, 3)
Min z: -9.50629, Max z: 8.48362
|
|
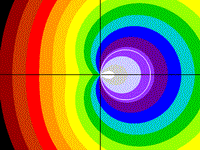
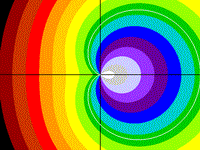
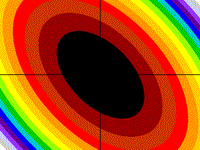
Black Hole
has only imaginary roots
z = x2 - xy + y2
Drawing Limits: (-2, -2) - (2, 2)
Min z: 0, Max z: 9.21882
|
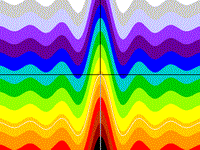 |
A Lonely Pulse
basically, y = sin(x)/x
z = 10 - (10sin(x) / x) - y
Drawing Limits: (-20, -20) - (20, 20)
Min z: -14.931, Max z: 27.1723
|
|
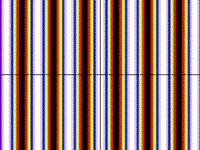
Vertical Bars
z = 10cos(x)
Drawing Limits: (-20, -20) - (20, 20)
Min z: -9.99919, Max z: 10
|
|
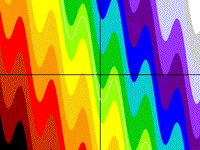
Zig Zag
basically, y = cos(x) + x
z = 5cos(x) + 2x - y
Drawing Limits: (-20, -20) - (20, 20)
Min z: -52.8971, Max z: 58.1044
|
|