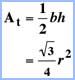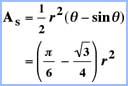Curves of Constant Width and Reuleaux Polygons

Observe the path of the triangle as it rotates. First, the path of the boundary is not a square at the four corners. But because the triangle rotates within a square, it is the basis for a square drill bit.

The behavior of the center is also fascinating. The center does not remain fixed and thus traces a path composed of four arcs of an ellipse.

This section features the

Constant Width Curves
or
Orbiform Curves.

They are also known as Reuleaux Polygons,

most often the triangle, or "Rollers."

Their well-known application is found in the

Wankel Engine

MATHEMATICA^®Code

Mathematica code

Reuleaux Polygons Code Part II

Historical Sketch:

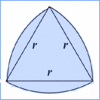
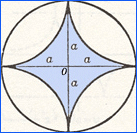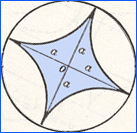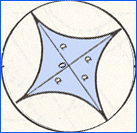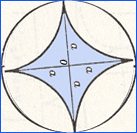Animation

A constant width curve is a planar convex oval with the property that the distance between two parallel tangents to the curve is constant. Visualize a circle inscribed in square with the circle rolling, or rotating in the square. The diameter of the circle is the same as the width of the square. The width of a closed convex curve is defined to be the distance between the parallel lines bounding it. The parallel lines of the square are sometimes called "supporting lines." Please note, the inscribed asteroid does not fit the definition.

Some background is helpful. Unlike many plane curves, the constant width and Reuleaux polygon investigations are rooted in machine design and engineering. Moreover, compared to the history of most plane curves, this work is relatively young.

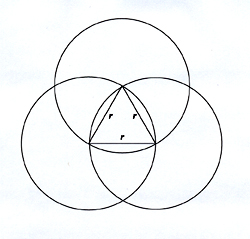
Franz Reuleaux (1829 - 1905) recognized that simple plane curves of constant width might be constructed from regular polygons with an odd number of sides. Thus, triangles and pentagons are frequently constructed using a corresponding number of intersecting arcs.

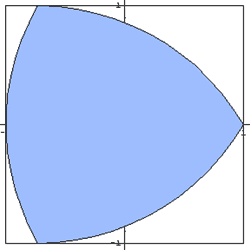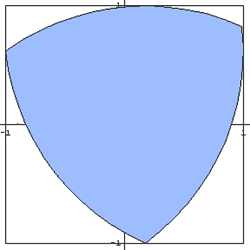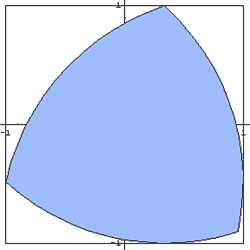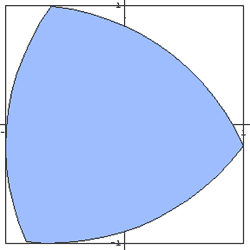
In engineering, Felix Heinrch Wankel (1902-1988) designed a rotor engine which has the shape of a Reuleaux triangle inscribed in a chamber, rather than the usual piston, cylinder, and mechanical valves. The rotor engine, now found in Mazda automobiles has 40% fewer parts and thus far less weight. Within the Wankel rotor, three chambers are formed by the sides of the rotor and the wall of the housing. The shape, size, and position of the chambers are constantly altered by the rotation of the rotor, i.e., the Reuleaux triangle or deltoid. _

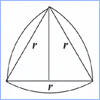
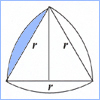
Areas

Area of the Triangle
Area of triangle equation

Using well-known 30⁰-60⁰-90⁰,

Area of a Segment
Segment equation

Total Area of a Reuleaux Triangle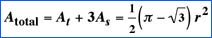

Additional MATHEMATICA® CODE

Other Useful Links and Books

For information on the Wankel engine: < http://en.wikipedia.org/wiki/Wankel_engine >

http://mathworld.wolfram.com/ReuleauxTriangle.html

Eves, Howard, AN INTRODUCTION TO THE HISTORY OF MATHEMATICS, 6th ed., Saunders College Publishing, 1992.

Gray, Alfred, Modern Differential Geometry of Curves and Surfaces with MATHEMATICA^®, 2nd ed., CRC Press, 1998.

Reuleaux, Franz, The Kinematics of Machinery, trans. A. Kennedy, Dover, 1963 (reprint of 1876 translation of 1875 German original).

Wagon, Stan, MATHEMATICA^®IN ACTION, W. H. Freeman and Co. ISBN 0-7167-2229-1 or ISBN 0-7167-2202-X (pbk.)

Wagon, Stan, MATHEMATICA^® IN ACTION, 2nd ed., Springer-Verlag, 2000. ISBN 0-387-98684-7

MATHEMATICA^® Code and animation contributed by

Luis Garcia
Matthew Nelson

updated 2007