Superconics + Spirals

Variations on a Theme by Euler .........

Other members of the Spiral Family of Plane Curves:
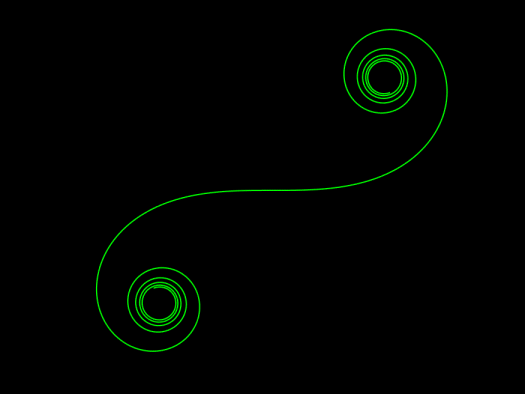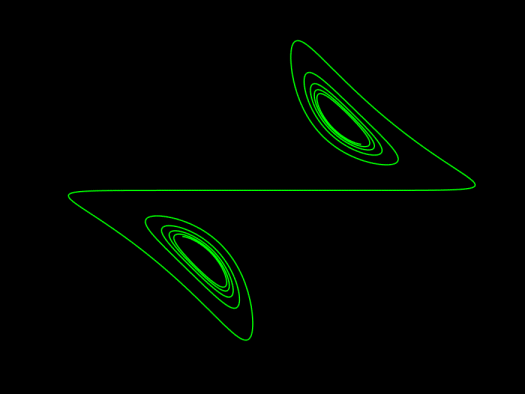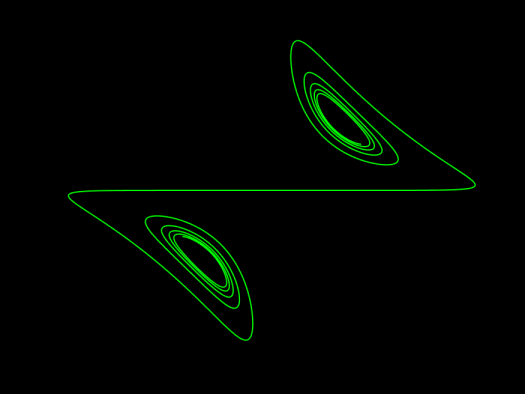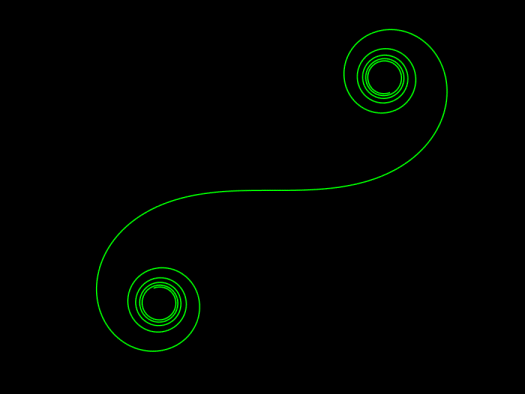
The Spirals of Archimedes, of Fermat, of Euler, of Cornu,
Hyperbolic, Logarithmic, Spherical, Parabolic, Nielsen's, Seiffert . . . .

Euler on a Swiss franc note.
1707 - 1783

Click here for the full article including the animation code and equations.

Many spirals are based on a simple circle, though modulated by a variable radius. We have generalized this concept by allowing the circle to be replaced by any closed curve that is topologically equivalent. In this note we focus on the superconics for the reasons that they are at once abundant, analytical, and aesthetically pleasing. We also demonstrate how the concept can be applied to random closed forms.

In addition to practical applications, spirals have a and lengthy and fascinating heritage. Among others, Euler studied spirals in 1781 in connection with his investigations of elastic springs. His mentor, Jakob Bernoulli was also interested. Later, Marie Alfred Cornu (1841-1902), a French engineer and scientist, studied the curves in conjunction with the diffraction of light. (French usually do not use "Marie" for its confusion with a female name.) Many publications by others soon followed.

Genesis of the Superspiral

"Without apology or embarrassment, he (Euler) treated these numbers (real and imaginary) as equal players upon the mathematical stage and showed how to take their roots, logs, sines, and cosines."

"In mathematics you don't understand things. You just get used to them."

W. Dunham in Euler: The Master of Us All

Johann von Neumann

References

Burchard, H. G. et al. (1994). "Approximation with Aesthetic Constraints," in Designing Fair Curves and Surfaces: Shape Quality in Geometric Modeling and Computer-aided Design, N. S. Sapidis, Ed., SIAM.

Dillen, F. (1990). "The Classification of Hypersurfaces of a Euclidean Space with Parallel Higher Order Fundamental Form," Mathematische Zeitschrift, 203: 635-643.

Olver, F.W. J., Lozier, D.W., Boisvert, R.F., and Clark, C.W., (2010). NIST Handbook of Mathematical Functions. Cambridge University Press.

Yoshida, N. and Saito, T. (2006). "Interactive Aesthetic Curve Segments," The Visual Computer, 22 (9), 896-905.

Ziatdinov, R., Yoshida, N., and Kim, T., (2012). Analytic parametric equations of log-aesthetic curves of incomplete gamma functions, Computer Aided Geometric Design, 29 (2), 129-140.

Zwikker, C. (1963). The Advanced Geometry of Plane Curves and Their Applications, Dover Press.

Waldman, C. H, (2016). Superconics < ../superconicncb/superconicncb.htm >

Waldman, C. H., Chyau, S. Z. and Gray, S. B. (2017). Superconics: Hypergeometric Functions (in preparation).

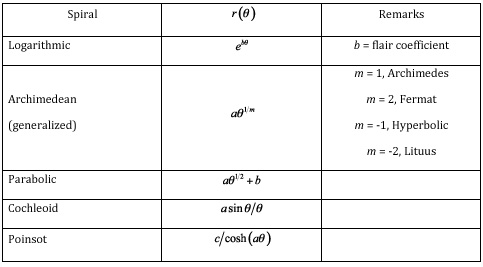
equations

from Jakob Bernoulli's famous spiral on his tomb in the cathedral at Basel, Switzerland.

Eadem mutata resurgo.
I shall arise the same though changed.

Other Waldman contributions to the NCB:
Sinusoidal Spirals: < ..//waldman/waldman.htm >
Bessel Functions < ..//waldman2/waldman2.htm >
Gamma Funcions < ..//waldman3/waldman3.htm >
Polynomial Functions < ..//waldman4/waldman4.htm >
Other spiral Deposits in the NCB:
< ..//spiral/spiral.htm >
< ..//log/log.htm >

2017