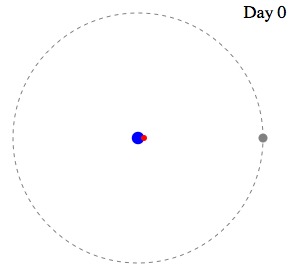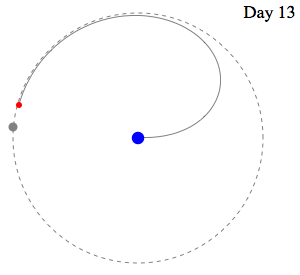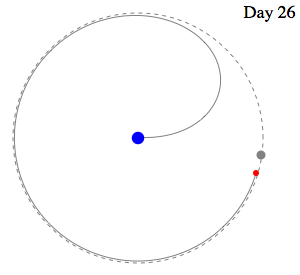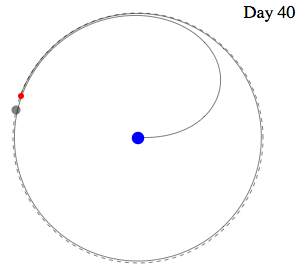
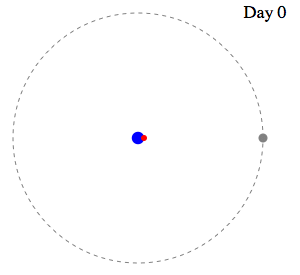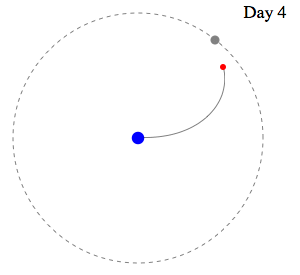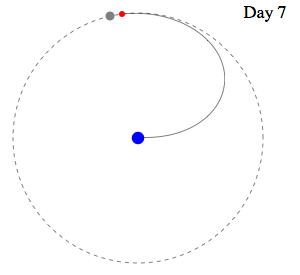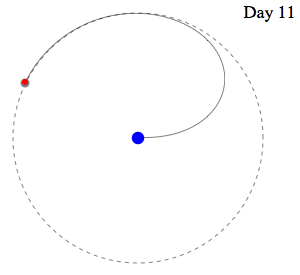
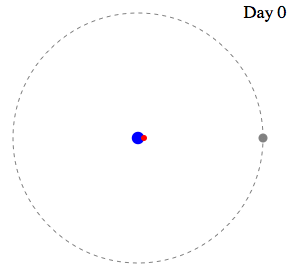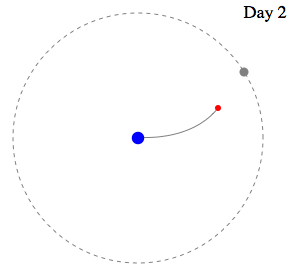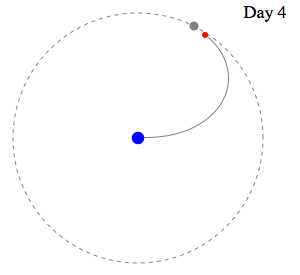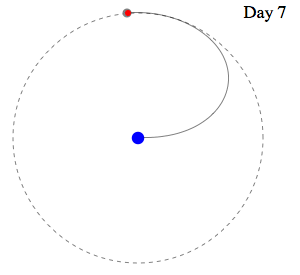
| Swan's
Speed < Moon's Speed
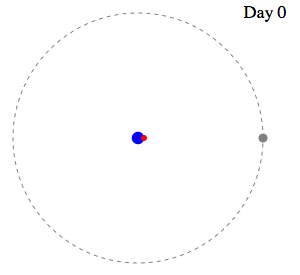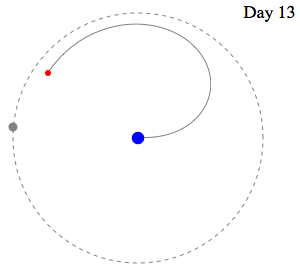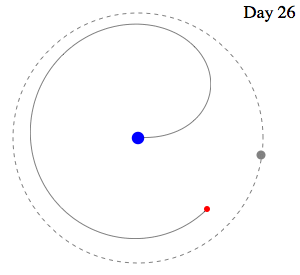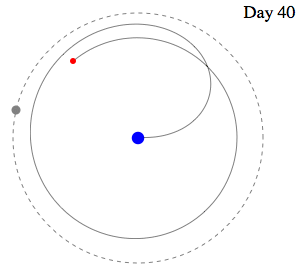
|
Swan's
Speed = Moon's Speed
|
What
is a "Pursuit Curve?"
One particle
travels along a specified
curve, while a second pursues it, with a
motion always directed toward
the first. The velocities of the two
particles are always in the
same ratio.
Thus,
the
two beads move with related
velocities. When the ratio k of
the two velocities
is greater than one ( k > 1 ),
the pursuer travels
faster than the pursued. The question then
becomes, "At
what point do the two meet?"
What is the
"capture" point?
|
Swan's
Speed slightly greater than Moon's Speed leads to
capture. . .
|
And an
even faster capture
|
Historical
Sketch:
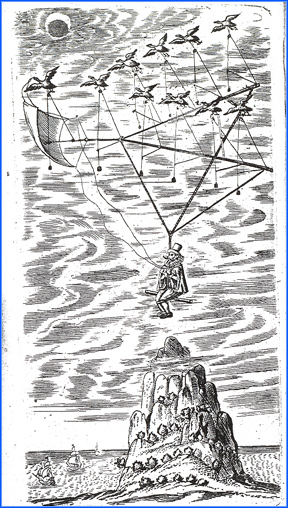
|
The
First
Story in English Literature of Space
Travel
Over 300 years before
Neil
Armstrong stepped on the moon, a bishop of the
Anglican church wrote
the first English language science fiction tale of
the voyage.
The story involved a flight to the moon by an
astronaut named Domingo
Gonsales, the "speedy messenger," in
a space "Engine" powered by
"wild swan" having "one foote with Clawes, talons
and pounces, like an
eagle", and the other being "on the whole like a
swan or water
fowle." He affectionally named his fictional
birds "Gansas"
with "gansa" being the German name for
"goose." His Gansas
migrated in much the same pattern as geese.
"Not many hours after the departure . . ., my
Gansas began to bestir
themselves, still directing their course toward
the globe or body of
the Mooon, and they made their way with that
incredible swiftness, as I
think they gained not so little as fifty Leagues
in every hour.
In The Man in
the Moone
Godwin clearly foreshadows the great scientific
discoveries of the 17th
century, including the rotation of the earth in
its orbit about the sun
and the law of gravity.
"Whereby
it
appeareth, not only that my Gansa's
took none other way than directly
toward the Moon, but also,
that when we rested (as at first we
did for many hours), either we were
insensibly carried, (for I perceived
no such motion) round about the
Globe of the Earth, or else that
(according to the late opinion of
Copernicus,) the Earth is carried
about, and turneth round perpetually,
from West to East. . . ."
|
(On looking back toward Earth)
| ". . .the
farther we went, the less of the globe
of the Earth appeared to us,
whereas, . . . the Moon showed herself
more and more monstrously huge. . . .On
the Moon we
discerned certain spots or clouds, as it
were, so did I then in the
earth. But where as the form of
those spots in the Moon continue
constantly one and the same, these
(spots) little & little
did change every hour. The reason
thereof I conceive to be
this. That
whereas the Earth, according to her
natural motion, ( for that such a
motion he hath, I am now constrained to
join in the opinion with
Copernicus), turneth round upon her own
axis every 24 hours from the
West to the East. . . ." |
The Earth was .
. . "no
other than
a huge Mathematical Globe, leisurely turned
before me, wherein
successively, all the countries of our earthly
world within the compass
of 24 hours. Philosophers and
Mathematicians, I . . . now
confess the wilfulness of their own
blindness. They have made the
world believe hitherto, that the Earth hath no
motion."sage in this volent flight, I
perceived that we began
to approach near unto another Earth, if I
amy so call it, being the
globe or very bopais
volent flight, I perceived that we began
to approach near unto another Earth, if I
amy so call it, being the
globe or very body of that star we call the
Moon."
Godwin's
mathematics
included having the birds fly at
a constant rate on a nonlinear outward
trajectory of more than 11 days.
The return to Earth
took 8 days but followed a straight
line. Modern
history of mathematics
students will marvel at the accuracy of
Godwin's speculative knowledge
of science in 1638. His story published
after
Columbus and Kepler, but before much of
Galileo's publicity, includes
specific references to Copernicus and no
mention of Newton who was yet
unborn. Godwin wrote he lived in the
"Age of Discovery."
|
The landing . .
.

|
"After
eleven days passage in this
violent flight, I perveived that we
began to approach near unto another
Earth, if I may so call it, being the
Globe or very body of that star
which we call the Moon. I
perceived also that it was covered for
the most
part with a huge mighty sea . . . ."
"The first difference that I found
between it and our earth, was, that
it showed itself in its natural
colors. Ever after I was free
from the attraction of the Earth,
whereas with us, a thing removed from
our eye but a league or two, begins to
put on that lurid and deadly
color of blue."
"How often did I wish myself . .
.that freely I might fill the world with
the fame of my glory and
renown."
|

Francis
Godwin (1562-1633)
Bishop of Llandaff and
Hereford
|
|
Andrew
Simoson of King College in Tennesse recognized this story
provided a great opportunity to introduce pursuit curves
and MATHEMATICA® animations to
entice modern students
to think about space travel. In other passages
Godwin's
mathematics included having the geese fly at
a constant rate on an outward trajectory that was not
linear and lasted
12 days.
Important
Reference Points for an Historic
Overview
c.
45 BC
|
Zeno
|
The
paradox of
Achilles' pursuit of a tortoise.
|
c.
174 AD
|
Lucian
|
The
True History
A comic satire on travel to the
moon by sailing on a waterspout.
|
c.
1300
|
Dante
|
The
Divine Comedy
Beatrice and Dante fall
upwards from a
mountaintop on Earth to tour the
solar system.
|
1452-1519
|
Leonardo
da Vinci
|
|
1543
|
Copernicus
|
De
Revolutionibus Orbium Coelestium
|
c.
1620-30
|
Johannes
Kepler
|
The
Dream or
Somnium
|
c.
1630
|
Galileo
|
Calculated
a
ball would fall from the moon to
the Earth in3 hours, 22 minutes,
and 4
seconds. |
c.
1599
1638
|
Francis
Godwin
Bishop and Historian
(1562-1633)
|
The
Man
in the Moone.
Published posthumously by a
friend. The first story of
space travel in English
literature. By 1768 at least
25 editions are know to have
existed in a wide variety of
languages.
|
1656
|
Cyrano
de Bergerac
|
Voyage
to the Moon
|
1749
|
Pierre
Bouguer
|
Figure
de la terre déterminée
|
| 1943 |
Antoine
de Saint-Exupéry
|
The
Little Prince
|
July
20, 1969
|
Neil
Armstrong
|
"One
small
step for man, one giant leap for
mankind."
|
|
|
|
While still a student in
1593
Kepler wrote a series of
speculations on the geography of
the
moon. Later in 1610,
Galileo sent him an early copy
of The
Starry
Messenger.
Kepler replied, ". . . for those
who will come shortly to attempt
this
journey (to the moon), let us
establish the astronomy;
Galileo,
you of Jupiter, I of the moon."
|
|
The opportunities
for
animation of pursuit curves are
enormous. The NCB invites faculty
and students to try their hand at some of
these problems as class
projects. Then hopefully you will add a
"choice" effort to our
NCB MATH Archive collection as a sampler of a
fun activity from your
campus.
|
|


