Unicursal and Multicursal Graphs

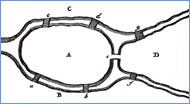
Euler Circuit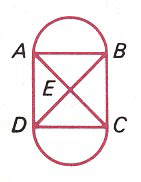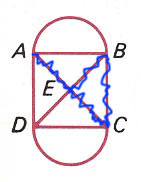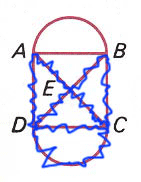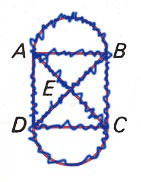

Because all vertices or nodes are "even," a traversable network may be traced starting and ending at the same letter. This illustration starts and ends at A but any of the letters might have been selected.

Euler Path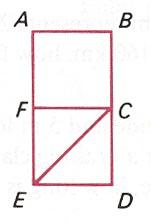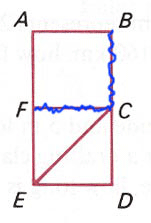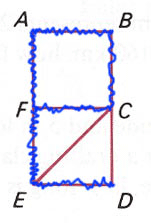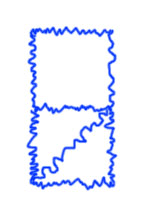

This graph has exactly two odd vertices, F and E. This illustration starts at F and ends at E. We also might have started at E and ended at F.

Euler Paths and Circuits

If a graph has more than two vertices of odd degree, then there is no Euler Path or Circuit for the graph.

If each of the vertices of a connected graph has even degree, then there is an Euler Circuit for the graph. No matter which vertex is selected as a starting point, a route may be traced crossing each path once and only once, and ending by returning to the starting vertex. A graph with only even nodes can be traversed unicursally by a route that both starts and ends at the same point.

If a connected graph has exactly two odd vertices, then an Euler Path may be traced crossing each path once and only once, but the starting point must be one of the odd vertices and the ending point will be the other of the odd vertices. In other words, if a graph has exactly two odd nodes, then it can be traversed unicursally by starting at one of the odd nodes and then terminating at the other.

A graph with more than two odd nodes is said to be non-traversable, or multicursal. In other words, routes will have to be traced more than once.

Interesting Facts . . . .

"Unicursal" and "multicursal" graphs are basic concepts in topology and are not truly curves. Nevertheless, many students might know these terms as part of graph theory and will enjoy seeing animations of the most important types, an Euler Circuit and an Euler Path.

Euler's 1736 paper on the bridges of Königsberg is widely recognized as the origin of graph theory.

Euler was prompted to investigate the 'calculus of position' by a letter from the mayor of Danzig in Prussia (now Gdansk in Poland), some 80 miles west of Königsberg. Euler replied to the mayor that this type of problem "bears little relationship to mathematics, and I do not understand why you expect a mathematician to produce it......(M)ost noble Sir, you have assigned this question to the geometry of position, but I am ignorant as to what this new discipline involves..."

Euler, being the genius that he was, clearly was captivated. Soon thereafter he wrote an Italian mathematician . . . .

"A problem was posed to me about an island in the city of Königsberg, surrounded by a river spanned by seven bridges, and I was asked whether someone could traverse the separate bridges in a connected walk in such a way that each bridge is crossed only once.....This question is so banal, but seemed to be worthy of attention in that geometry, nor algebra, nor even the art of counting was sufficient to solve it. In view of this, it occurred to me to wonder whether it belonged to the geometry of position which Leibniz had once so much longed for. And so, after some deliberation, I obtained a simple, yet completely established, rule with whose help one can immediately decided for all examples of this kind, with any number of bridges in any arrangement ...."

Leonhard Euler to Giovanni Marinoni
March 13, 1736

Useful Links and Books	Euler is one of a number of distingished mathematicians born in Basel, Switzerland. Note the Euler formula for polyhedra.
Related material also in the National Curve Bank: ..//graphtheory/grthelink/grthelink.htm
Brian Hopkins and Robin J. Wilson, "The Truth about Königsberg," The College Mathematics Journal, Vol. 35, No. 3, May 2004, pp. 198-207. [Note: The NCB thanks Hopkins and Wilson for their invaluable historical source and translations.]
Bell, E. T., Men of Mathematics, Simon and Schuster, 1937, p. 118.
Eves, Howard, An Introduction to the History of Mathematics, 6th ed,. The Saunders College Publishing, 1990, pp. 460-461.
Katz, Victor J., A History of Mathematics, PEARSON - Addison Wesley, 2004, pp. 396-399.