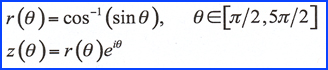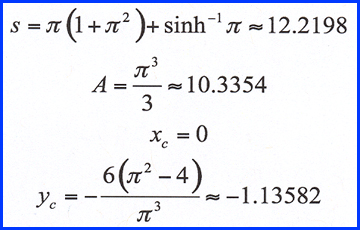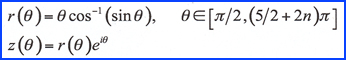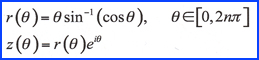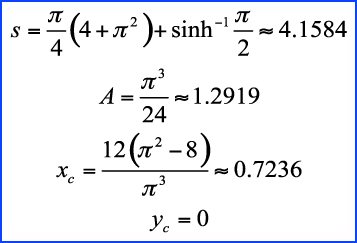Cye Waldman has found a plane curve,
previously unknown to the NCB, that renders
a credible heart shape and spiral. We
present this to the mathematics community
for comment. The "heart" is defined by
a polar equation and is also shown in the
complex form. At the NCB we have dubbed this
as "Cœur d'Cye" or "Waldman's Heart." We
solicit your comments.
|
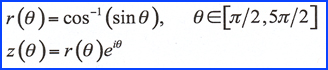
|
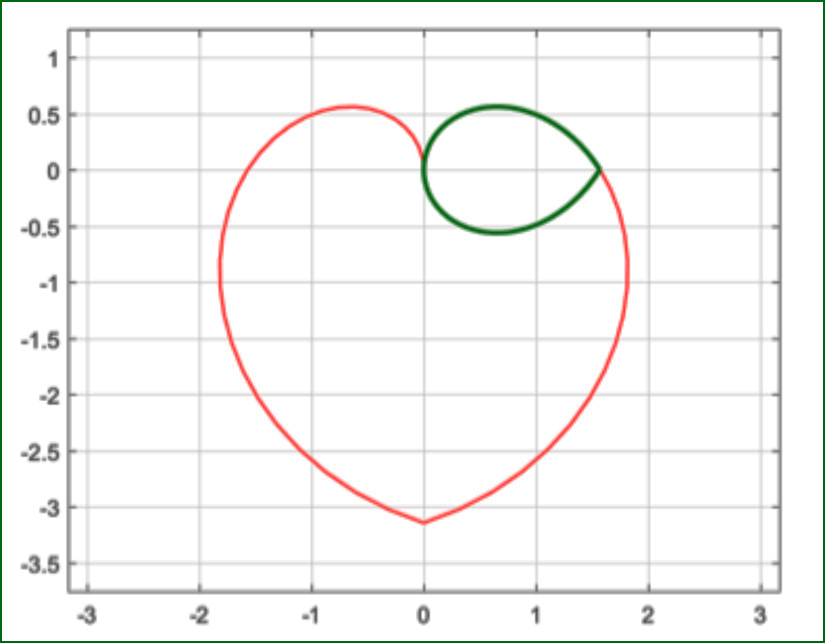
| The angular range was selected to
position the cusp of the heart at the
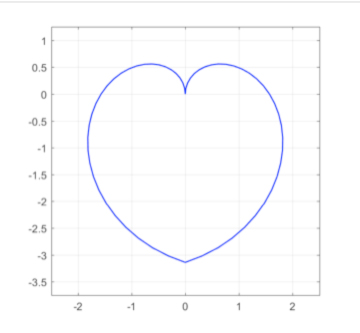
origin. The figure below shows the
heart. |
|
The arc length, area and centroid of
this heart can be found analytically. To
wit,
|
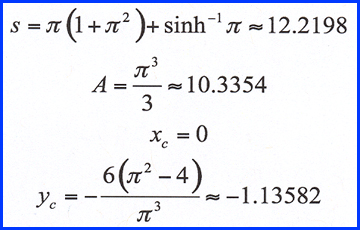
|
| In order to
turn this into a spiral, consider |
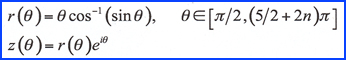
|
| The animations
below show that the heart is imperfect as the
spiral begins, but approaches the desired
shape after a few turns. |
The figure below shows
the application of the heart model in a
three-dimensional rendering.
|
Naturally, we
were curious as to the effect of switching the
sine and cosine in the above equation.
To that end, let
|
|
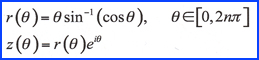
The result is a
leaf-shaped figure that is
shown in the
animation on the right where it is
overlaid on the heart for
comparison. Also note the
difference in the angular range.
|
|
| The equations
for the leaf are given as follows: |
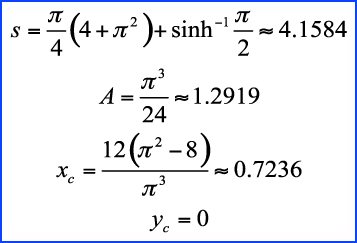 |
Notice the
leaf's area is just one-eighth of
the heart. |
|
 2018
2018