Click here for the full
article.
|
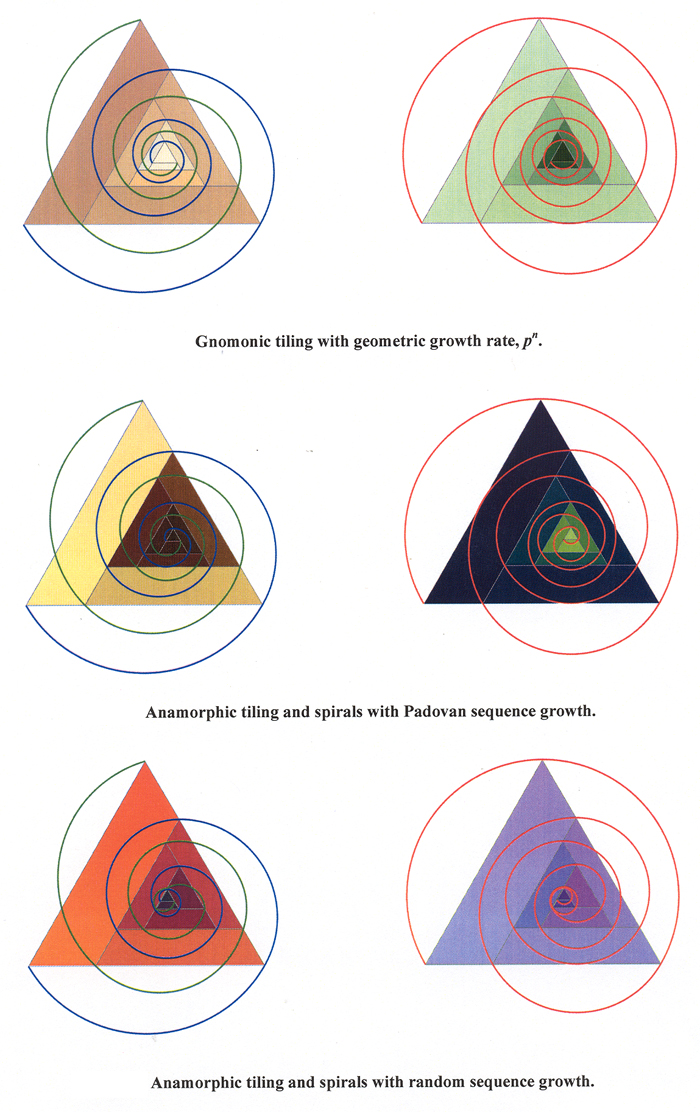
We are
familiar with the concept of
gnomonic tiling in which a figure
added to another reproduces the
shape of the original. The process
can repeated over and over to form a
tessellated mosaic that covers the
plane. The initial tile is called
the seed and the added
piece is called the gnomon.
The gnomons generally increase in
size geometrically, i.e., by a power
law. Figures thus created are called
whorled
figures, as the gnomons are usually
added in a circular fashion about
the seed. See, for example, Gazalé
[1] and Waldman [2].
|
|
Our Figure 1
|
There are
magnificent mosaics, or tilings, if
you prefer, that continue to amaze
us. In this paper
we consider a particular whorled
triangle and demonstrate that it can
be generalized to arbitrary, indeed,
even random growth, provided that the
growth is monotonic. Thus we can
create anamorphic tilings for which
the ‘gnomons’ are all of different
shapes, albeit within the same general
family. Here, we are using the term
anamorphic in the optical sense of
having unequal magnifications along
two axes perpendicular to each
other. We show a generic
anamorphic tiling and a single spiral.
In fact, we demonstrate that these
tilings support three different
spirals and comment on the nature of
those spirals.
|
|
|
|
|