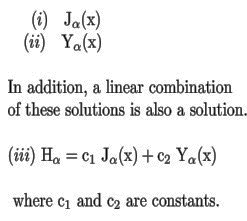The Differential Equations of Friedrich Wilhelm Bessel

Bessel Functions of the First Kind of Integer Order "n"

One of the highest honors a mathematician may earn is to be remembered centuries later by a widely utilized proof or equation.
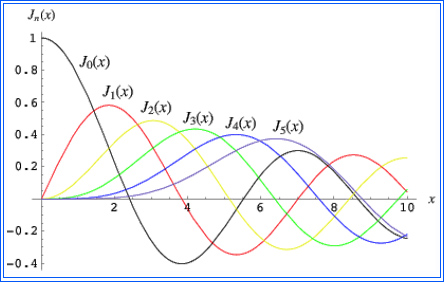
Thus we honor the German astronomer Friedrich Wilhelm Bessel for the many applications of his second-order differential equations.

We now investigate his equation "of the first kind" with discussion of the solution.

Because a Bessel Function is of the second order differential equation, it should have two linearly-independent solutions.

Because a simple, or general, definition does not exist, the few points at which exact values are known are tabulated in various references along with various other properties. Otherwise values are often computed using commerical software products.

from the base of the pendulum . . .

Bessel is so famous for his outstanding work in mathematics that his contributions to astronomy are sometimes ignored. In particular, his publication on the pendulum in 1828 is virtually a "writer's guide" of how to present good science in the early 19th century. He acknowledges his predecessors, describes his methods, builds his equipment, collects the data, refines his experiment and then concludes with his results. In this particular publication he was attempting to "fine tune" a pendulum to have exactly one swing occur in precisely one second of time.

References and Comments

Binner, David, < http://www.akiti.ca/Mathfxns.html >.

Bessel, Friedrich Wilhelm, Untersuhungen über die Länge des einfachen Secundenpendels . . .,Berlin, Akademie der Wissenschaften, 1828.

Bowman, Frank, Introduction to Bessel Functions, Dover Publications, 1958.

Watson, G. N., A Treatise on the Theory of Bessel Functions, 2nd ed., Cambridge Univesity Press, 1966.

Weisstein, Eric., Bessel Function of the First Kind, < http://mathworld.wolfram.com/BesselFunction.html > .

The NCB is grateful to the Huntington Library for permission to use Bessel's illustrations in this article. < http://catalog.huntington.org>

Bessel curves may be created using Mathematica®.