1.
The implicit equation in the xy-plane
is
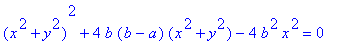where a and b are positive
constants. This is a curve with
reflectional symmetry about both the
horizontal and vertical axes.
2. Any Hippopede is the intersection
of a torus with one of its tangent planes
that is parallel to its axis of rotational
symmetry, as demonstrated in the animation.
3. Converting the implicit equation
to polar coordinates gives
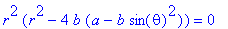so the origin at r = 0 is
a solution, and the remainder of the curve is
given by
 .
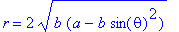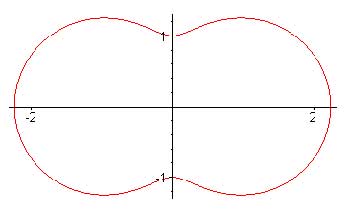
4. If 0 < b<
a, the point at the origin is
an isolated node and the balance of the
solution set is a simple closed curve, also
called an Elliptic Lemniscate
of Booth.
The b < a
special
case is given by the rational
parametrization
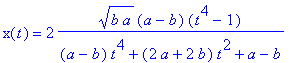
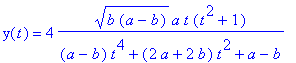
Each of these curves is the image of an
ellipse under an inversion in a
circle. The circle and the ellipse
must have the same center. The curve
is non-convex for b <
a < 2b, and
convex for a > 2b
when the shape is oval, but is not exactly a
strictly defined ellipse.
5. If a = b,
the quartic implicit equation factors into
two quadratics; thus, the curve is the
union of two circles, centered at ( - b,0 )
and ( b, 0 ), each of radius b,
and mutually tangent at the origin.
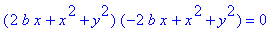
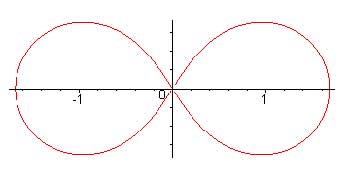
6. If 0 < a
< b, the curve
intersects itself at the origin, and it is
also called a Hyperbolic Lemniscate
of Booth.This is given by
the rational parametrization
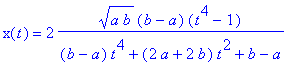
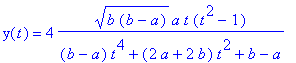
Each of these curves
is the image of a hyperbola under an
inversion in a circle. The
circle and the hyperbola must have the
same center.
|
The
animation.
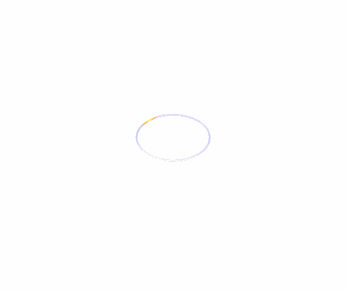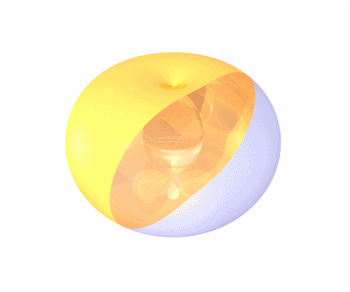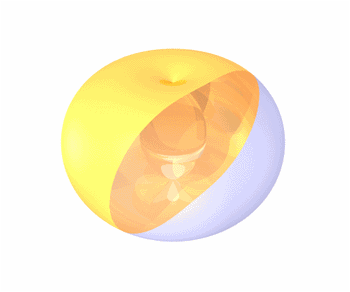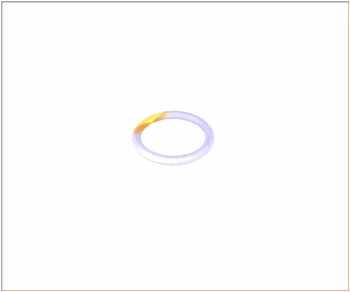
Now that
you have investigated the equations and
read of the special properites, we
suggest you use the "Reload" or
"Refresh" button at the top of your
computer. This will replay the
animation. Visually "slice" the
torus to see the plane lemniscate evolve
into a pair of circles, and then the
oval shape.
and
|
