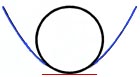
|
The word "osculate" means "to
kiss." A succession of circles that converge
to snuggly "kiss" a curve are said to be osculating
circles. They are also known as the Circle of Curvature.
 The
tangent
to a point on a curve was applied by the
earliest investigators to study the derivative and
thus Calculus. Just as the tangent line
approximates a curve at a point, the osculating
circle is an even better approximation by capturing
the curvature. |
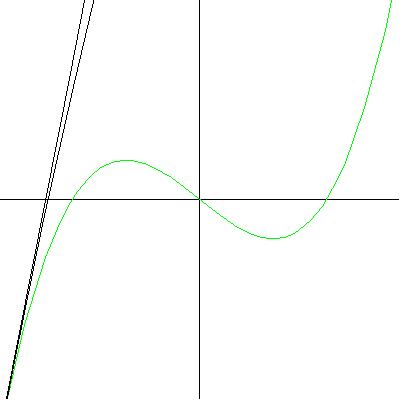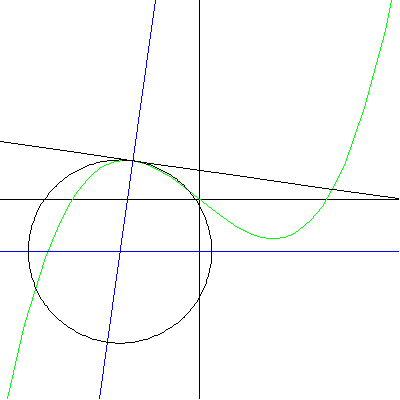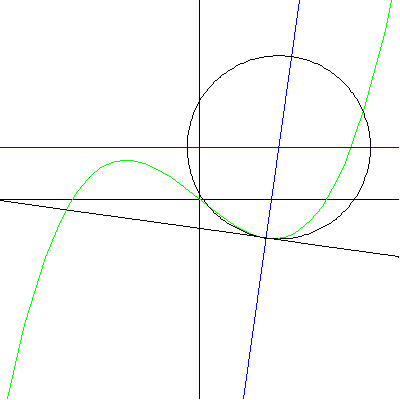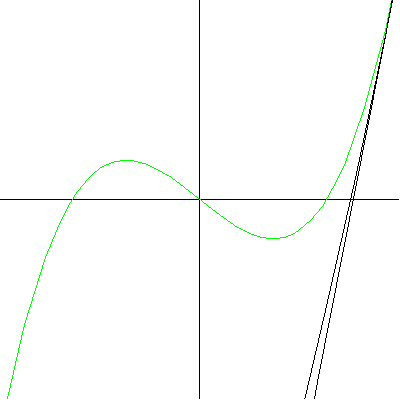  Note that at the point of inflection (second derivative), the tangent must jump across the curve; thus, the circle also jumps across this curve. Replay the animation to watch the jump at (0,0). In our MATHEMATICA® animations, both the tangent and normal lines are drawn at the point of contact of the curve and the circle. |
Our
animations
feature several
Classic
Curves We ask you
to recall the construction for circumscribing a circle
about a triangle. 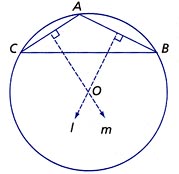 A minimum of
three points on the
curve are needed to determine, first the
perpendicular bisectors, and then the center and
radius of the osculating circle. As the
three points on a given curve move closer together -
converge to a single point - the radius of the circle
becomes the normal to the tangent at the point.  Play this animation. As the
three points on the parabola converge to the vertex,
the circle of curvature takes on a radius and center
containing the normal to the point of tangency.
|
 |
 y = sin (x), a tangent, normal, and osculating circle. |
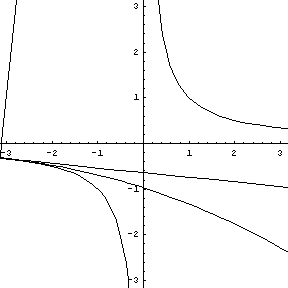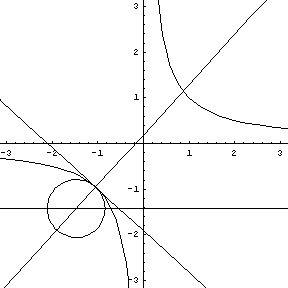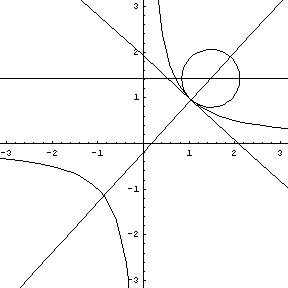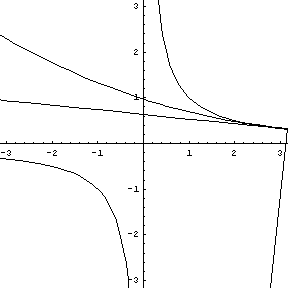  Replay this animation. |
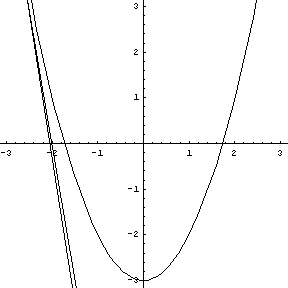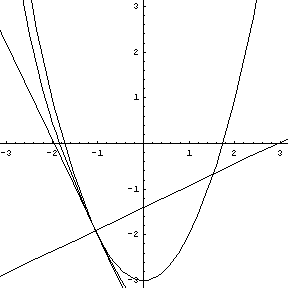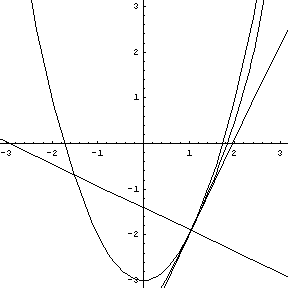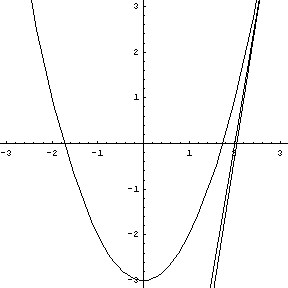  Replay this animation. |
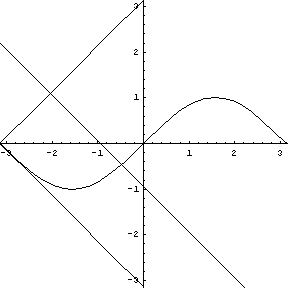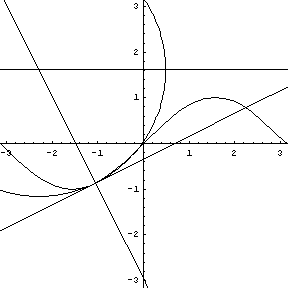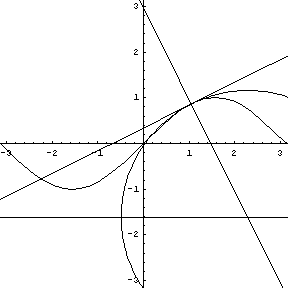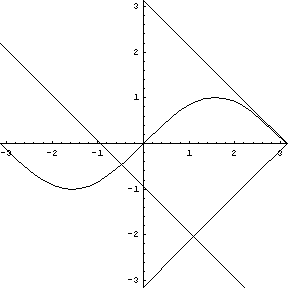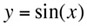  Replay this animation. |
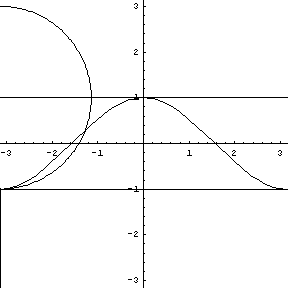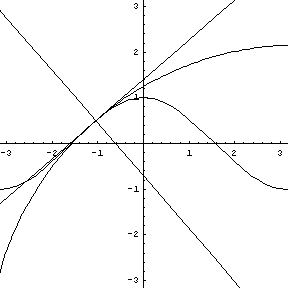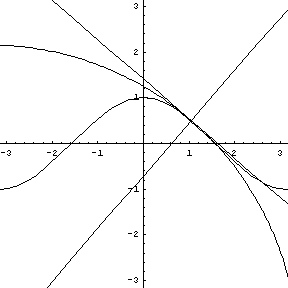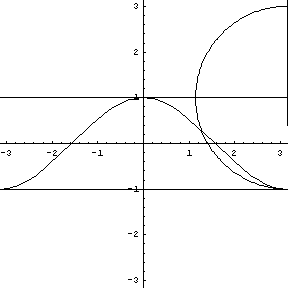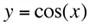  Replay this animation. |
  |
|
|
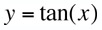Suggestions
for
the MATHEMATICA® code are on this link. |
|
|
|
 |
| Eves, Howard, AN INTRODUCTION TO THE
HISTORY OF MATHEMATICS, 6th ed., Saunders
College Publishing, 1992, p. 405. Leibniz
"defined the osculating circle and showed its
importance in the study of curves."
A large statue of Leibniz is at the Royal Academy of Arts in the heart of fashionable London. Note the English chose to spell his name as . . . .  . |
|
| Gray, Alfred, Modern Differential Geometry of
Curves and Surfaces with MATHEMATICA®, 2nd ed.,
CRC Press, 1998, pp. 111-115. |
|
| Wagon, Stan, MATHEMATICA®IN ACTION, W.
H. Freeman and Co., 1991. ISBN
0-7167-2229-1 or ISBN
0-7167-2202-X (pbk.) Wagon, Stan, MATHEMATICA® IN ACTION, 2nd ed., Springer-Verlag, 2000. ISBN 0-387-98684-7 for other animations. |
|
| Yates, Robert C., Curves and Their Properties,
NCTM,
1952, pp. 60-63. |