How many roots does the following equation have?
sin x = log10 x
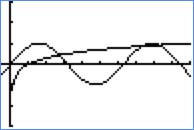
The equation sin x = log10 x has exactly three real roots.
Recall that the log (10) = 1 and sin (x) ≤ 1. Thus, 0 ≤ x ≤ 10 must contain one complete period of the sine function and part of a second period.
For x = 10, know that log(10) = 1 and that 1 ≥ sin (x). The log function intercepts the sine function three times.
Previous Problem | Next Problem

